-

Sub-harmonic Bifurcation Analysis of Single-Walled Carbon Nanotube Based Mass Sensor
Liangqiang Zhou,
Shanshan Liu,
Fangqi Chen
Issue:
Volume 5, Issue 3, June 2016
Pages:
97-102
Received:
7 June 2016
Published:
8 June 2016
Abstract: Bifurcation behaviors are very important for the design of sensors. Using the sub-harmonic Melnikov method, the sub-harmonic bifurcation of single-walled carbon nanotube based mass sensor is investigated in this paper. The parametric conditions for sub-harmonic bifurcation of this system are obtained. It is presented that when the ratio of the excitation amplitude to the damping coefficient crosses a critical value, sub-harmonic bifurcations of m order (odd) can occur. The stability conditions of the bifurcation solution for the system parameters are also obtained by using the affection-angle transformation and average method. The result can provide some guidance for the design of this class of sensors.
Abstract: Bifurcation behaviors are very important for the design of sensors. Using the sub-harmonic Melnikov method, the sub-harmonic bifurcation of single-walled carbon nanotube based mass sensor is investigated in this paper. The parametric conditions for sub-harmonic bifurcation of this system are obtained. It is presented that when the ratio of the exci...
Show More
-

On the Line Successive Overrelaxation Method
I. K. Youssef,
Salwa M. Ali,
M. Y. Hamada
Issue:
Volume 5, Issue 3, June 2016
Pages:
103-106
Received:
17 May 2016
Accepted:
30 May 2016
Published:
13 June 2016
Abstract: A line version of the KSOR method is introduced, LKSOR method. Comparison of the performance of some different iterative techniques with their line format (Jacobi – Gauss Seidel and SOR) are considered. Implementation of LKSOR method for several different formulas in different mesh geometries is discussed. The proposed method considers the advantages of the LSOR in addition to those of the KSOR. A graphical representation of the behavior of the spectral radius near the optimum value illustrates the smoothness in the selection of relaxation parameters.
Abstract: A line version of the KSOR method is introduced, LKSOR method. Comparison of the performance of some different iterative techniques with their line format (Jacobi – Gauss Seidel and SOR) are considered. Implementation of LKSOR method for several different formulas in different mesh geometries is discussed. The proposed method considers the advantag...
Show More
-

Development of a Hybrid Algorithm for Efficiently Solving Mixed Integer-Continuous Optimization Problems
Issue:
Volume 5, Issue 3, June 2016
Pages:
107-113
Received:
14 June 2016
Published:
15 June 2016
Abstract: Problems with mixed integer-continuous design variables are a class of complicated optimization problems that commonly exist in practical engineering design work. In this paper, a hybrid algorithm combining metamodel-based Multipoint Approximation Method (MAM) and Hooke-Jeeves direct search technique is presented to efficiently seek the optimum solutions for mixed integer-continuous optimization problems. First, optimal continuous values are obtained by the Sequential Quadratic Programming method (SQP) on the approximated functions in a current trust region. Then, continuous values are rounded to the nearest integer values for discrete variables. Utilizing integer values as a starting point, the Hooke-Jeeves assisted MAM is applied to search for the discrete optimal solution in the sub-space of discrete variables as well as accordingly update the sub-optimal values for continuous design variables by SQP. The proposed hybrid algorithm is examined by the well established benchmark example and the obtained results demonstrate the superiority of the developed algorithm over GA in terms of computational cost and the quality of solutions.
Abstract: Problems with mixed integer-continuous design variables are a class of complicated optimization problems that commonly exist in practical engineering design work. In this paper, a hybrid algorithm combining metamodel-based Multipoint Approximation Method (MAM) and Hooke-Jeeves direct search technique is presented to efficiently seek the optimum sol...
Show More
-

A Continuous-Time Multi-Agent Systems Based Algorithm for Constrained Distributed Optimization
Ping Liu,
Huaqing Li,
Liping Feng
Issue:
Volume 5, Issue 3, June 2016
Pages:
114-120
Received:
25 May 2016
Accepted:
7 June 2016
Published:
18 June 2016
Abstract: This paper considers a second-order multi-agent system for solving the non-smooth convex optimization problem, where the global objective function is a sum of local convex objective functions within different bound constraints over undirected graphs. A novel distributed continuous-time optimization algorithm is designed, where each agent only has an access to its own objective function and bound constraint. All the agents cooperatively minimize the global objective function under some mild conditions. In virtue of the KKT condition and the Lagrange multiplier method, the convergence of the resultant dynamical system is ensured by involving the Lyapunov stability theory and the hybrid LaSalle invariance principle of differential inclusion. A numerical example is conducted to verify the theoretical results.
Abstract: This paper considers a second-order multi-agent system for solving the non-smooth convex optimization problem, where the global objective function is a sum of local convex objective functions within different bound constraints over undirected graphs. A novel distributed continuous-time optimization algorithm is designed, where each agent only has a...
Show More
-

Application of the Adomian Decomposition Method to Oscillating Viscous Flows
Issue:
Volume 5, Issue 3, June 2016
Pages:
121-132
Received:
3 June 2016
Accepted:
13 June 2016
Published:
29 June 2016
Abstract: In this paper three oscillating viscous flows are studied by applying the Adomian decomposition method (ADM). Major improvement is on the choice of the assignment of the first term of the decomposition series. Different from past studies in which the initial velocity profile of the whole domain is assigned as the first term of the decomposition series, the assignment in present study is simply the boundary velocity for Stokes’ second problem and the pressure gradient for pulsatile flows. This improvement demonstrates and implies that ADM is not only good in approaching the known exact solution, but also possesses the practicability in treating realistic problems. The derived approximate solutions accurate up to any order can be obtained after two key parameters are determined. Present results show an excellent agreement with those calculated by the exact solutions. Based on the present results, more periodic problems can be analyzed by ADM with the help of Fourier analysis.
Abstract: In this paper three oscillating viscous flows are studied by applying the Adomian decomposition method (ADM). Major improvement is on the choice of the assignment of the first term of the decomposition series. Different from past studies in which the initial velocity profile of the whole domain is assigned as the first term of the decomposition ser...
Show More
-

Several Kinds of Chromatic Numbers of Multi-fan Graphs
Issue:
Volume 5, Issue 3, June 2016
Pages:
133-137
Received:
10 July 2016
Published:
11 July 2016
Abstract: Coloring problem is a classical difficult problem of graph theory. It is a fundamental problem in scientific computation and engineering design. In recent years, a variety of graph coloring problems frequently appeared and solved many problems in production. It is a difficult problem to discuss the chromatic number of a given graph class. In the paper, we introduce several kinds of chromatic numbers of graphs such as adjacent-vertex-distinguishing total chromatic number, adjacent-vertex-distinguishing proper edge chromatic number, smarandachely-adjacent-vertex-distinguishing edge chromatic number, and the multi-fan graphs are considered.
Abstract: Coloring problem is a classical difficult problem of graph theory. It is a fundamental problem in scientific computation and engineering design. In recent years, a variety of graph coloring problems frequently appeared and solved many problems in production. It is a difficult problem to discuss the chromatic number of a given graph class. In the pa...
Show More
-

The Wiener Index and the Hosoya Polynomial of the Jahangir Graphs
Shaohui Wang,
Mohammad Reza Farahani,
M. R. Rajesh Kanna,
Muhammad Kamran Jamil,
R. Pradeep Kumar
Issue:
Volume 5, Issue 3, June 2016
Pages:
138-141
Received:
21 April 2016
Accepted:
3 May 2016
Published:
13 July 2016
Abstract: Let G be a simple connected graph having vertex set V and edge set E. The vertex-set and edge-set of G denoted by V(G) and E(G), respectively. The length of the smallest path between vertices u,v 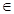 V(G) is called the distance, d(u,v), between the vertices u,v. Mathematical chemistry is the area of research engaged in new application of mathematics in chemistry. In mathematics chemistry, we have many topological indices for any molecular graph, that they are invariant on the graph automorphism. In this research paper, we computing the Wiener index and the Hosoya polynomial of the Jahangir graphs J 5,m for all integer number m ≥3. The Wiener index is the sum of distances between all pairs of vertices of G as W(G)=
V(G) is called the distance, d(u,v), between the vertices u,v. Mathematical chemistry is the area of research engaged in new application of mathematics in chemistry. In mathematics chemistry, we have many topological indices for any molecular graph, that they are invariant on the graph automorphism. In this research paper, we computing the Wiener index and the Hosoya polynomial of the Jahangir graphs J 5,m for all integer number m ≥3. The Wiener index is the sum of distances between all pairs of vertices of G as W(G)= 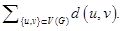 And the Hosoya polynomial of G is H(G,x)=
And the Hosoya polynomial of G is H(G,x)= 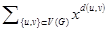 , where d(u,v) denotes the distance between vertices u and v.
Abstract: Let G be a simple connected graph having vertex set V and edge set E. The vertex-set and edge-set of G denoted by V(G) and E(G), respectively. The length of the smallest path between vertices u,v
, where d(u,v) denotes the distance between vertices u and v.
Abstract: Let G be a simple connected graph having vertex set V and edge set E. The vertex-set and edge-set of G denoted by V(G) and E(G), respectively. The length of the smallest path between vertices u,v 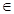 V(G) is called the distance, d(u,v), between the vertices u,v. Mathematical chemistry is the area of research engaged in new application of mathematics in...
Show More
V(G) is called the distance, d(u,v), between the vertices u,v. Mathematical chemistry is the area of research engaged in new application of mathematics in...
Show More
-

Solving a Class of Nonlinear Delay Integro–differential Equations by Using Differential Transformation Method
Mohammad Bagher Moghimi,
Abdollah Borhanifar
Issue:
Volume 5, Issue 3, June 2016
Pages:
142-149
Received:
30 April 2016
Accepted:
14 June 2016
Published:
13 July 2016
Abstract: In this paper, differential transformation method is used to find exact solutions of nonlinear delay integro– differential equations. Many theorems are presented that required for applying differential transformation method for nonlinear delay integro–differential equation. The validity and efficiency of the proposed method are demonstrated through several tests.
Abstract: In this paper, differential transformation method is used to find exact solutions of nonlinear delay integro– differential equations. Many theorems are presented that required for applying differential transformation method for nonlinear delay integro–differential equation. The validity and efficiency of the proposed method are demonstrated through...
Show More
-

Distributed Subgradient Algorithm for Multi-agent Convex Optimization with Local Constraint Sets
Qingguo Lü,
Huaqing Li,
Li Xiao
Issue:
Volume 5, Issue 3, June 2016
Pages:
150-159
Received:
12 June 2016
Accepted:
20 June 2016
Published:
13 July 2016
Abstract: This paper considers a distributed constrained optimization problem, where the objective function is the sum of local objective functions of distributed nodes in a network. The estimate of each agent is restricted to different convex sets. To solve this optimization problem which is not necessarily smooth, we study a novel distributed projected subgradient algorithm for multi-agent optimization with nonidentical constraint sets and switching topologies. The algorithm shows that each agent minimizes its own objective function while communicating information locally with other agents over a network with time-varying topologies but satisfying a standard connectivity property. Under the assumption that the network topology is weight-balanced, the novel distributed subgradient algorithm we proposed is proven to be convergent. Particularly, we suppose the step-size is various, which is different from previous work on multi-agent optimization that makes worst-case assumption with constant step-size.
Abstract: This paper considers a distributed constrained optimization problem, where the objective function is the sum of local objective functions of distributed nodes in a network. The estimate of each agent is restricted to different convex sets. To solve this optimization problem which is not necessarily smooth, we study a novel distributed projected sub...
Show More
-

The Numerical Solution of the TVD Runge-Kutta and WENO Scheme to the FPK Equations to Nonlinear System of One-Dimension
Wang Wenjie,
Feng Jianhu,
Xu Wei
Issue:
Volume 5, Issue 3, June 2016
Pages:
160-164
Received:
19 June 2016
Accepted:
27 June 2016
Published:
23 July 2016
Abstract: Firstly, it was studied to the Fokker-Planck-Kolmogorov (FPK) equations for nonlinear stochastic dynamic system. Secondly, it was discussed to the third-order TVD Runge-Kutta difference scheme totime for differitial equations and the fifth-order WENO scheme for differitial operators. And combined he third-order TVD Runge-Kutta difference scheme with the fifth-order WENO scheme, obtained the numerical solution for FPK equations using the TVD Runge-Kutta WENO scheme. Finally, the numerical solution was compared with the analytic solution for FPK equations. The numerical method is shown to give accurate results and overcomes the difficulties of other methods, such as: the big value of probability density function at tail etc.
Abstract: Firstly, it was studied to the Fokker-Planck-Kolmogorov (FPK) equations for nonlinear stochastic dynamic system. Secondly, it was discussed to the third-order TVD Runge-Kutta difference scheme totime for differitial equations and the fifth-order WENO scheme for differitial operators. And combined he third-order TVD Runge-Kutta difference scheme wit...
Show More
-

The Application of Matrix in Control Theory
Issue:
Volume 5, Issue 3, June 2016
Pages:
165-168
Received:
23 July 2016
Published:
25 July 2016
Abstract: This paper presents a new way to justify the controllability of linear ordinary systems. This way is based on the maximum geometric multiplicity of eigenvalues for the coefficient matrix of the linear ordinary equation. This method is equivalent to other discrimination laws for controllability.










