-

A Highly Accurate Approximation of Conic Sections by Quartic Bézier Curves
Zhi Liu,
Na Wei,
Jieqing Tan,
Xiaoyan Liu
Issue:
Volume 5, Issue 2, April 2016
Pages:
40-45
Received:
18 February 2016
Accepted:
26 February 2016
Published:
9 March 2016
Abstract: A new approximation method for conic section by quartic Bézier curves is proposed. This method is based on the quartic Bézier approximation of circular arcs. We give the upper bound of Hausdorff distance between the conic section and the quartic Bézier curve, and also show that the approximation order is eight. And we prove that our approximation method has a smaller upper bound than previous quartic Bézier approximation methods. A quartic G2-continuous spline approximation of conic sections is obtained by using the subdivision scheme at the shoulder point of the conic section.
Abstract: A new approximation method for conic section by quartic Bézier curves is proposed. This method is based on the quartic Bézier approximation of circular arcs. We give the upper bound of Hausdorff distance between the conic section and the quartic Bézier curve, and also show that the approximation order is eight. And we prove that our approximation m...
Show More
-

Oscillation of Second Order Nonlinear Differential Equations with a Damping Term
Xue Mi,
Ying Huang,
Desheng Li
Issue:
Volume 5, Issue 2, April 2016
Pages:
46-50
Received:
23 March 2016
Published:
25 March 2016
Abstract: A class of second-order nonlinear differential equations with a damping term is investigated in this paper. By using the Riccati transformation technique and general weight functions, we obtain some new sufficient conditions for the oscillation of the equation. Our results improve and extend some known results. Two examples are given to illustrate the main results.
Abstract: A class of second-order nonlinear differential equations with a damping term is investigated in this paper. By using the Riccati transformation technique and general weight functions, we obtain some new sufficient conditions for the oscillation of the equation. Our results improve and extend some known results. Two examples are given to illustrate ...
Show More
-

The Stability of High Order Max-Type Difference Equation
Han Cai-hong,
Li Lue,
Tan Xue
Issue:
Volume 5, Issue 2, April 2016
Pages:
51-55
Received:
6 April 2016
Published:
7 April 2016
Abstract: In this paper, we investigate the stability of following max-type difference equation
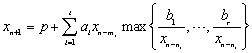
, where
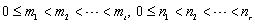
, with
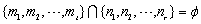
,
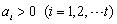
,
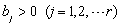
and
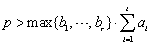
, the initial values are positive. By constructing a system of equations and binary function, we show the equation has a unique positive equilibrium solution, and the positive equilibrium solution is globally asymptotically stable. The conclusion of this paper extends and supplements the existing results.
-

Effect of Grid Step Sizes on Computational Time Using Finite-Difference Method for Seismic Wave Modeling
Olowofela Joseph. A.,
Akinyemi Olukayode. D.,
Ajani Olumide. O.
Issue:
Volume 5, Issue 2, April 2016
Pages:
56-63
Received:
5 September 2015
Accepted:
21 September 2015
Published:
15 April 2016
Abstract: Finite-difference method, a popular seismic forward modeling method is a technique which allows us to numerically solve partial differential equations like the wave equation solved in this paper. Beyond its use in standard data acquisition, it is a very instructive tool to understand how waves propagate in the earth's subsurface. Since the accuracy obtainable by using the finite difference scheme lies solely on its stability and ability to handle grid dispersion, this is achievable by applying appropriate grid step sizes. The developed finite-difference method was employed to generate snapshots of synthetic seismograms to highlight the effect of grid step sizes on computational time while ensuring numerical stability of the scheme used through accurate discretization of the medium and adopting Perfectly Matched Layer (PML) absorbing boundary conditions. Results shows that for a grid size of 5m x 5m x 5m having 260 x 260 x 100 grid points and time step of 100 - 500, the wavefield propagating is horizontally symmetric. From the results, the importance of grid step sizes on computational time is re-emphasized.
Abstract: Finite-difference method, a popular seismic forward modeling method is a technique which allows us to numerically solve partial differential equations like the wave equation solved in this paper. Beyond its use in standard data acquisition, it is a very instructive tool to understand how waves propagate in the earth's subsurface. Since the accuracy...
Show More
-

Comparison Solutions Between Lie Group Method and Numerical Solution of (RK4) for Riccati Differential Equation
Sami H. Altoum,
Salih Y. Arbab
Issue:
Volume 5, Issue 2, April 2016
Pages:
64-72
Received:
17 February 2016
Accepted:
25 March 2016
Published:
15 April 2016
Abstract: This paper introduced Lie group method as a analytical method and then compared to RK4 and Euler forward method as a numerical method. In this paper the general Riccati equation is solved by symmetry group. Numerical comparisons between exact solution, Lie symmetry group and RK4 on these equations are given. In particular, some examples will be considered and the global error computed numerically.
Abstract: This paper introduced Lie group method as a analytical method and then compared to RK4 and Euler forward method as a numerical method. In this paper the general Riccati equation is solved by symmetry group. Numerical comparisons between exact solution, Lie symmetry group and RK4 on these equations are given. In particular, some examples will be con...
Show More
-

Julia and Mandelbrot Sets of the Gamma Function Using Lanczos Approximation
Richard Eneojo Amobeda,
Terhemen Aboiyar,
Solomon Ortwer Adee,
Peter Vanenchii Ayoo
Issue:
Volume 5, Issue 2, April 2016
Pages:
73-77
Received:
20 March 2016
Accepted:
29 March 2016
Published:
15 April 2016
Abstract: This work explores the Julia and Mandelbrot sets of the Gamma function by extending the function to the entire complex plane through analytic continuation and functional equations. Various Julia and Mandelbrot sets associated with the Gamma function are generated using the iterative function 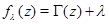 , with different parameter
, with different parameter 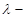 values. To produce an accurate result using the integral definition of the Gamma function, a large number of terms would have to be added during the numerical integration procedure; this makes computation of Gamma function a very difficult task. To overcome this challenge, the Lanczos approximation of the Gamma function which presents an efficient and easy way to compute algorithms for approximating the Gamma function to an arbitrary precision is used. The resulting images reveal that the fractal (chaotic) behaviour found in elementary functions is also found in the Gamma function. The chaotic nature of the Julia and Mandelbrot sets provides a way of understanding complexity in systems as well as just in shapes.
Abstract: This work explores the Julia and Mandelbrot sets of the Gamma function by extending the function to the entire complex plane through analytic continuation and functional equations. Various Julia and Mandelbrot sets associated with the Gamma function are generated using the iterative function
values. To produce an accurate result using the integral definition of the Gamma function, a large number of terms would have to be added during the numerical integration procedure; this makes computation of Gamma function a very difficult task. To overcome this challenge, the Lanczos approximation of the Gamma function which presents an efficient and easy way to compute algorithms for approximating the Gamma function to an arbitrary precision is used. The resulting images reveal that the fractal (chaotic) behaviour found in elementary functions is also found in the Gamma function. The chaotic nature of the Julia and Mandelbrot sets provides a way of understanding complexity in systems as well as just in shapes.
Abstract: This work explores the Julia and Mandelbrot sets of the Gamma function by extending the function to the entire complex plane through analytic continuation and functional equations. Various Julia and Mandelbrot sets associated with the Gamma function are generated using the iterative function 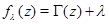 , with different parameter
, with different parameter 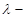 values. To produce an accurat...
Show More
values. To produce an accurat...
Show More
-

Tuncay Can’s Approximation Method to Obtain Initial Basic Feasible Solution to Transport Problem
Issue:
Volume 5, Issue 2, April 2016
Pages:
78-82
Received:
14 April 2016
Accepted:
27 April 2016
Published:
12 May 2016
Abstract: Obtaining an initial basic feasible solution to a transport problem – or a corner point in the convex polytope region – is extremely important in terms of reaching the optimal solution to the problem in the shortest time. When a transport problem is basically accepted as a linear programming problem, a degenerated solution is caused by the structure of the simplex method used when modelling with linear programming and located in a corner point sometimes at the optimal solution itself but mostly in close proximity to the optimal solution vector. One of the ways to eliminate this degenerated solution is to employ approximation methods. The main aim of this paper is to introduce Tuncay Can’s approximation method, which was developed as an alternative to the approximation methods in the literature for a balanced transport problem. Tuncay Can’s approximation method usually has less iterations than other approximation methods. In this paper, the Tuncay Can approximation method is introduced as an alternative to The North West Corner Rule, Minimum Cost Method, and the RAM and VAM methods.
Abstract: Obtaining an initial basic feasible solution to a transport problem – or a corner point in the convex polytope region – is extremely important in terms of reaching the optimal solution to the problem in the shortest time. When a transport problem is basically accepted as a linear programming problem, a degenerated solution is caused by the structur...
Show More
-

Application of Growth Functions to Describe the Dynamics of Avascular Tumor in Human Body
Bayru Haftu Hindeya,
Samba Narasimha Murthy
Issue:
Volume 5, Issue 2, April 2016
Pages:
83-90
Received:
20 April 2016
Accepted:
29 April 2016
Published:
12 May 2016
Abstract: This paper deals with the applications of mathematical growth functions such as monomolecular, time delay logistic and Gompertz functions to describe the dynamics of avascular tumor growth. In this case we analyze the steady state of the modified systems of the model using Jacobean matrix to show that it is stable on the nontrivial stationary points of each applications. Numerical simulation of the growth functions is implemented by using “ode45” in MATLAB and graphical outputs are presented to show differences in evaluation of tumor sub-populations. We also find that the tumor cells increases with time so that the nutrient is disproportional to the number of cells and they transform in to quiescent and necrotic cells that cause cancer.
Abstract: This paper deals with the applications of mathematical growth functions such as monomolecular, time delay logistic and Gompertz functions to describe the dynamics of avascular tumor growth. In this case we analyze the steady state of the modified systems of the model using Jacobean matrix to show that it is stable on the nontrivial stationary point...
Show More
-

Anti-periodic Boundary Value Problems of φ-Laplacian Impulsive Differential Equations
Issue:
Volume 5, Issue 2, April 2016
Pages:
91-96
Received:
3 May 2016
Accepted:
13 May 2016
Published:
30 May 2016
Abstract: This paper concerned with the existence of solutions of anti-periodic boundary value problems for impulsive differential equations with φ-Laplacian operator. Firstly, the definition a pair of coupled lower and upper solutions of the problem is introduced. Then, under the approach of coupled upper and lower solutions together with Nagumo condition, we prove that there exists at least one solution of anti-periodic boundary value problems for impulsive differential equations with φ-Laplacian operator.
Abstract: This paper concerned with the existence of solutions of anti-periodic boundary value problems for impulsive differential equations with φ-Laplacian operator. Firstly, the definition a pair of coupled lower and upper solutions of the problem is introduced. Then, under the approach of coupled upper and lower solutions together with Nagumo conditi...
Show More



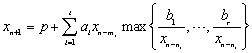 , where
, where 




