2024, Volume 13
2023, Volume 12
2022, Volume 11
2021, Volume 10
2020, Volume 9
2019, Volume 8
2018, Volume 7
2017, Volume 6
2016, Volume 5
2015, Volume 4
2014, Volume 3
2013, Volume 2
2012, Volume 1
Characterizations of Jordan *-derivations on Banach *-algebras
is a real or complex unital Banach *-algebra, 
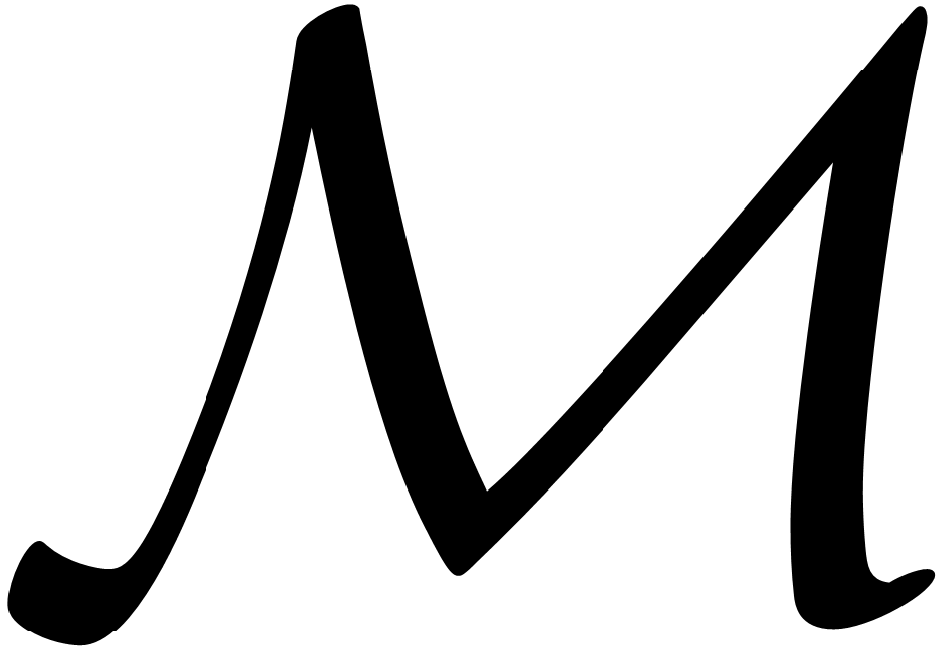
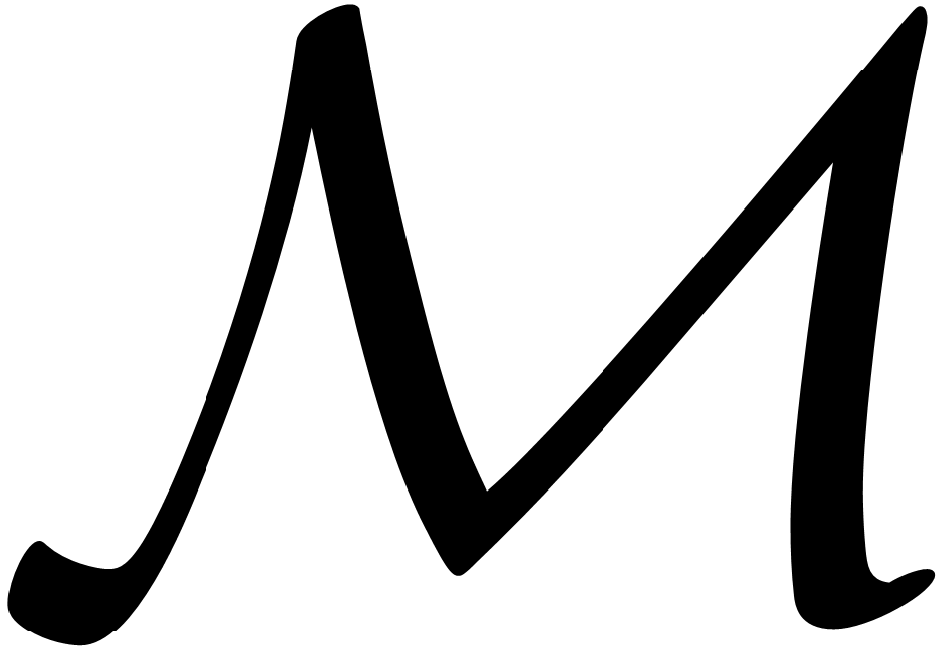
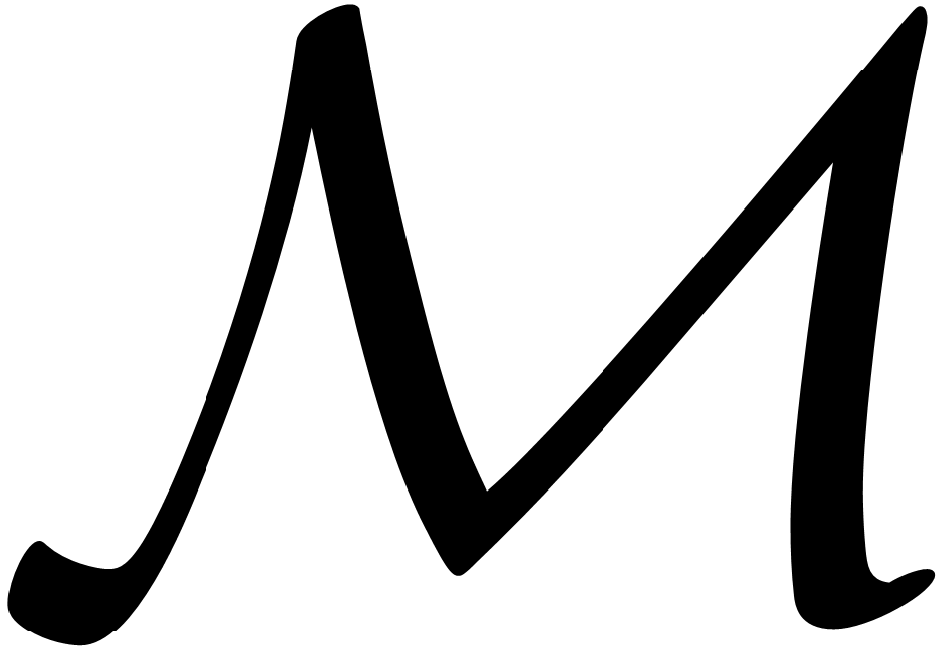
is a unital Banach -bimodule, and G ∈ is a left separating point of . In this paper, we investigate whether the additive mapping δ: → satisfies the condition A,B ∈ , AB = G ⇒ Aδ(B)+δ(A)B*= δ(G) characterize Jordan *-derivations. Initially, we prove that if is a real unital C*-algebra and G = I is the unit element in , then δ (non-necessarily continuous) is a Jordan *-derivation. In addition, we prove that if is a real unital C*-algebra and δ is continuous, then δ is a Jordan *-derivation. Finally, we show that if is a complex factor von Neumann algebra and δ is linear, then δ (non-necessarily continuous) is equal to zero.
Information
