-

Heavy Metals Pollution in Soil and Its Influence in South of Iraq
Luma Naji Mohammed Tawfiq,
Farah Feasal Ghazi
Issue:
Volume 2, Issue 3, September 2017
Pages:
59-63
Received:
27 January 2017
Accepted:
18 February 2017
Published:
9 March 2017
DOI:
10.11648/j.dmath.20170203.11
Downloads:
Views:
Abstract: The aim of this paper is to determine the significant levels of some heavy metals such: lead, chromium, nickel and cadmium, were determined. Sources of pollution and their distribution according to presence of elements in the soils over the whole zone of the province of Maysan in southern of Iraq were investigated 36 soil samples from different zones: residential, industrial, commercial, agricultural and main roads, were collected from the soil surface and a depth of 30 cm and analyzed measuring of concentrations for heavy metals by a device ICP-MS technique. The results were compared with global standard levels of these elements in the soil.
Abstract: The aim of this paper is to determine the significant levels of some heavy metals such: lead, chromium, nickel and cadmium, were determined. Sources of pollution and their distribution according to presence of elements in the soils over the whole zone of the province of Maysan in southern of Iraq were investigated 36 soil samples from different zon...
Show More
-

Some Aspects of Certain Form of Near Perfect Numbers
Bhabesh Das,
Helen K. Saikia
Issue:
Volume 2, Issue 3, September 2017
Pages:
64-67
Received:
29 January 2017
Accepted:
7 March 2017
Published:
24 March 2017
DOI:
10.11648/j.dmath.20170203.12
Downloads:
Views:
Abstract: It is well known that a positive integer n is said to be near perfect number, if σ(n) = 2n+d where d is a proper divisor of n and function σ(n) is the sum of all positive divisors of n In this paper, we discuss some results concerning with near perfect numbers from known near perfect numbers.
-

Refined Numerical Simulation of Environmental Flow, Mixing and Transport in Amazon River Near Manaus City Closed by Multiple Turbulence Models
Issue:
Volume 2, Issue 3, September 2017
Pages:
68-79
Received:
5 February 2017
Accepted:
3 March 2017
Published:
24 March 2017
DOI:
10.11648/j.dmath.20170203.13
Downloads:
Views:
Abstract: This paper reports a refined numerical simulation for Amazon River, aiming to develop a mathematical model and numerical tool for modeling and predicting turbulence flows and contaminant transport in complex natural waters. In the mathematical model, the depth-averaged two-equation closure turbulence 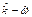 model, together with
model, together with 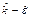 model and
model and 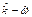 model, were used to close non-simplified quasi 3D hydrodynamic fundamental governing equations. The discretized equations, however, were solved by advanced multi-grid iterative method under coarse and fine two-levels’ non-orthogonal body-fitted grids with collocated variable arrangement. Except for steady flow and transport computation, the processes of black-water inpouring and plume development, caused by the side-discharge from the Negro River, also have been numerically studied. The used three depth-averaged two-equation closure models are suitable for modeling strong mixing turbulence. The recently built
model, were used to close non-simplified quasi 3D hydrodynamic fundamental governing equations. The discretized equations, however, were solved by advanced multi-grid iterative method under coarse and fine two-levels’ non-orthogonal body-fitted grids with collocated variable arrangement. Except for steady flow and transport computation, the processes of black-water inpouring and plume development, caused by the side-discharge from the Negro River, also have been numerically studied. The used three depth-averaged two-equation closure models are suitable for modeling strong mixing turbulence. The recently built 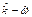 turbulence model with higher order of magnitude of transported variable
turbulence model with higher order of magnitude of transported variable 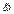 provides a possibility to enhance the computational precision. Based on the developed mathematical model, which can provide multiple turbulence two-equation closure models for quasi 3D modeling, a CFD software, namely Q3drm1.0 and Q3drm2.0, was developed. This numerical tool focuses on the refined numerical simulations of the steady and unsteady problems of flow and transports with the strong ability to deal with different tipes of discharges. In this paper, only the investigation of side-discharge is presented.
Abstract: This paper reports a refined numerical simulation for Amazon River, aiming to develop a mathematical model and numerical tool for modeling and predicting turbulence flows and contaminant transport in complex natural waters. In the mathematical model, the depth-averaged two-equation closure turbulence
provides a possibility to enhance the computational precision. Based on the developed mathematical model, which can provide multiple turbulence two-equation closure models for quasi 3D modeling, a CFD software, namely Q3drm1.0 and Q3drm2.0, was developed. This numerical tool focuses on the refined numerical simulations of the steady and unsteady problems of flow and transports with the strong ability to deal with different tipes of discharges. In this paper, only the investigation of side-discharge is presented.
Abstract: This paper reports a refined numerical simulation for Amazon River, aiming to develop a mathematical model and numerical tool for modeling and predicting turbulence flows and contaminant transport in complex natural waters. In the mathematical model, the depth-averaged two-equation closure turbulence 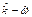 model, together with
model, together with 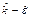 model and
model and 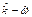 model, were us...
Show More
model, were us...
Show More
-

Some Explicit and Hybrid Strong Convergence Algorithms for Solving the Multiple-Sets Split Feasibility Problem
Peiyuan Wang,
Jianjun Zhou,
Risheng Wang,
Jie Chen
Issue:
Volume 2, Issue 3, September 2017
Pages:
80-87
Received:
6 February 2017
Accepted:
1 March 2017
Published:
24 March 2017
DOI:
10.11648/j.dmath.20170203.14
Downloads:
Views:
Abstract: In this paper, we present several explicit and hybrid strong convergence algorithms for solving the multiple-sets split feasibility problem (MSSFP). Firstly, we modify the existing successive, parallel and cyclic algorithms with the hybrid steepest descent method; then two new hybrid formulas based on the Mann type method are presented; Two general hybrid algorithms which can cover the former ones are further proposed. Strong convergence properties are investigated, and numerical experiments shows the compromise is promising.
Abstract: In this paper, we present several explicit and hybrid strong convergence algorithms for solving the multiple-sets split feasibility problem (MSSFP). Firstly, we modify the existing successive, parallel and cyclic algorithms with the hybrid steepest descent method; then two new hybrid formulas based on the Mann type method are presented; Two general...
Show More
-

Solution of the Hyperbolic Partial Differential Equation on Graphs and Digital Spaces: A Klein Bottle a Projective Plane and a 4D Sphere
Issue:
Volume 2, Issue 3, September 2017
Pages:
88-94
Received:
1 February 2017
Accepted:
28 February 2017
Published:
29 March 2017
DOI:
10.11648/j.dmath.20170203.15
Downloads:
Views:
Abstract: This paper studies the structure of the hyperbolic partial differential equation on graphs and digital n-dimensional manifolds, which are digital models of continuous n-manifolds. Conditions for the existence of solutions are determined and investigated. Numerical solutions of the equation on graphs and digital n-manifolds are presented.
-

A Coupling Method of Regularization and Adomian Decomposition for Solving a Class of the Fredholm Integral Equations Within Local Fractional Operators
Issue:
Volume 2, Issue 3, September 2017
Pages:
95-99
Received:
9 February 2017
Accepted:
13 March 2017
Published:
29 March 2017
DOI:
10.11648/j.dmath.20170203.16
Downloads:
Views:
Abstract: In this paper, we will apply the combined regularization-Adomian decomposition method within local fractional differential operators to handle local fractional Fredholm integral equation of the first kind. Theoretical considerations are being discussed. To illustrate the ability and simplicity of the method, some examples are provided. The iteration procedure is based on local fractional derivative. The obtained results reveal that the proposed methods are very efficient and simple tools for solving local fractional integral equations.
Abstract: In this paper, we will apply the combined regularization-Adomian decomposition method within local fractional differential operators to handle local fractional Fredholm integral equation of the first kind. Theoretical considerations are being discussed. To illustrate the ability and simplicity of the method, some examples are provided. The iteratio...
Show More
-

Effective Approach for Code Coverage Using Monte Carlo Techniques in Test Case Selection
Varun Jasuja,
Rajesh Kumar Singh
Issue:
Volume 2, Issue 3, September 2017
Pages:
100-106
Received:
20 February 2017
Accepted:
13 March 2017
Published:
29 March 2017
DOI:
10.11648/j.dmath.20170203.17
Downloads:
Views:
Abstract: Source code analysis alludes to the profound examination of source code and/or gathered form of code with a specific end goal to help discover the imperfections as far as security, comprehensibility, understanding and related parameters. In a perfect world, such systems consequently discover the defects with such a high level of certainty that what's found is surely a blemish. Notwithstanding, this is past the best in class for some sorts of utilization security defects. In this manner, such devices much of the time serve as helps for an examiner to help them focus in on security pertinent segments of code so they can discover blemishes all the more productively, instead of a device that just consequently discovers imperfections. Code Coverage is a measure used to portray the extent to which the source code of a system is tried by a specific test suite. A project with high code scope has been all the more completely tried and has a lower shot of containing software bugs than a system with low code scope. A wide range of measurements can be utilized to ascertain code scope; the absolute most fundamental are the percent of system subroutines and the percent of project articulations called amid execution of the test suite. This research work focus on the quality of source code using code coverage and analysis techniques. In the proposed research work, an effective model based approach shall be developed and implemented to improve the performance of code in terms of overall code coverage time, code complexity and related metrics.
Abstract: Source code analysis alludes to the profound examination of source code and/or gathered form of code with a specific end goal to help discover the imperfections as far as security, comprehensibility, understanding and related parameters. In a perfect world, such systems consequently discover the defects with such a high level of certainty that what...
Show More
-

Several Remarks on q-Binomial Inverse Formula and Examples
Issue:
Volume 2, Issue 3, September 2017
Pages:
107-111
Received:
22 January 2017
Accepted:
20 March 2017
Published:
13 April 2017
DOI:
10.11648/j.dmath.20170203.18
Downloads:
Views:
Abstract: In this paper, we first give some comments on the paper [J. Goldman and G. C. Rota, on the foundations of combinatorial theory IV finite vector spaces and Eulerian generating functions, Stud. Appl. Math., 49: 239--258 (1970)]. In that paper, Goldman and Rota showed two incorrect inversion formulas in Section 3. We point out the formulas and give the correct versions with the proof in this this paper first. Then we give some remarks on -binomial inverse formula concerning its applications.
Abstract: In this paper, we first give some comments on the paper [J. Goldman and G. C. Rota, on the foundations of combinatorial theory IV finite vector spaces and Eulerian generating functions, Stud. Appl. Math., 49: 239--258 (1970)]. In that paper, Goldman and Rota showed two incorrect inversion formulas in Section 3. We point out the formulas and give th...
Show More
-

Computing Certain Topological Indices of Generalised Mycielskian Graphs
Issue:
Volume 2, Issue 3, September 2017
Pages:
112-118
Received:
10 February 2017
Accepted:
24 March 2017
Published:
14 April 2017
DOI:
10.11648/j.dmath.20170203.19
Downloads:
Views:
Abstract: The generalized Mycielskians are the generalization of the Mycielski graphs, which were introduced by Mycielski in 1955. A topological index is a numeric parameter mathematically derived from a graph and is invariant under automorphism of graphs. Topological indices are widely used for establishing correlations between the structure of a molecular compound and its different physico-chemical properties. This paper investigates different degree-based topological indices of the generalized Mycielskians of G.
Abstract: The generalized Mycielskians are the generalization of the Mycielski graphs, which were introduced by Mycielski in 1955. A topological index is a numeric parameter mathematically derived from a graph and is invariant under automorphism of graphs. Topological indices are widely used for establishing correlations between the structure of a molecular ...
Show More








