For nuclei with 54≤Z≤60 and 86≤N≤94, the results regarding the excitation spectra at low energies, both in positive and negative parity, as well as the transition probabilities for electric dipole (B(E1)), quadrupole (B(E2)), and octupole transitions (B(E(3)), indicate the emergence of significant octupole behavior. These observations have been made using the Interacting Boson Model-1 (IBM-1). The study examines the onset of octupole deformation and its impact on the spectroscopic characteristics in even-even neutron-rich lanthanide isotopes, specifically in the Ba and Nd nuclei. The investigation compares the results obtained from the Interacting Boson Model-1 (IBM-1) with the existing experimental data. The focus is on understanding how the addition of neutrons influences the development of octupole deformation and its manifestation in the observed spectroscopic features. The onset of strong octupolarity for Z≈ 56 and N ≈ 88 nuclei is indicated by the results obtained for the electric dipole, quadrupole, and octupole transition probabilities, as well as the low-energy positive and negative-parity excitation spectra. Conversely, discrepancies between the spectroscopic data and the IBM results suggest that the mapping quality needs to be evaluated in order to determine if the mapped boson Hamiltonian or the fermionic calculations are the source of the issues.
| Published in | American Journal of Modern Energy (Volume 10, Issue 2) |
| DOI | 10.11648/j.ajme.20241002.11 |
| Page(s) | 18-24 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
IBM, Energy Levels, Electromagnetic Octupole Transitions
 remains conserved and is equal to half the number of valence nucleons.
remains conserved and is equal to half the number of valence nucleons.  (1)
(1) 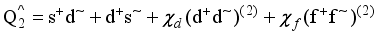 (2)
(2)  (3)
(3)  (4)
(4)  term, the term proportional to
term, the term proportional to 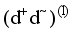
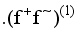 have been overlooked
have been overlooked 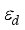 ,
,  , κ2, ρ,
, κ2, ρ, 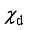 ,
,  , κ3, and χ3 of the
, κ3, and χ3 of the 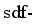 IBM Hamiltonian are chosen so that, in the boson condensate state, the expected value of the
IBM Hamiltonian are chosen so that, in the boson condensate state, the expected value of the 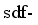 IBM Hamiltonian is in the vicinity of the global minimum
IBM Hamiltonian is in the vicinity of the global minimum 3.1. Energy Spectra
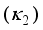 .
. 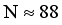 , the excitation energies of the expected negative-parity bands decrease. This neutron number corresponds to the point where the 3- excitation energy reaches its minimum value for most of the studied isotopic chains. However, as
, the excitation energies of the expected negative-parity bands decrease. This neutron number corresponds to the point where the 3- excitation energy reaches its minimum value for most of the studied isotopic chains. However, as 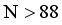 N exceeds 88, the excitation energy of the negative-parity levels gradually increases. However, in the case of Ba isotopes, the excitation energies of the negative-parity states remain constant until N = 92. This indicates that Ba isotopes with neutron numbers ranging from 86 to 92 indeed possess an octupole-deformed ground state. Similar results are obtained for the Ce isotopes. In the case of Xe and Nd isotopes, the anticipated levels around N = 88 and 90 display a nearly parabolic pattern. This systematic behavior of the negative-parity states suggests a moderate evolution of octupole collectivity in the neutron-rich lanthanide region. However, when compared to experimental data, the predicted negative-parity bands for Ba and Xe isotopes consistently exhibit elongation. The underlying reason for this observation is the same as that discussed for the positive-parity states depicted in Figure 1.
N exceeds 88, the excitation energy of the negative-parity levels gradually increases. However, in the case of Ba isotopes, the excitation energies of the negative-parity states remain constant until N = 92. This indicates that Ba isotopes with neutron numbers ranging from 86 to 92 indeed possess an octupole-deformed ground state. Similar results are obtained for the Ce isotopes. In the case of Xe and Nd isotopes, the anticipated levels around N = 88 and 90 display a nearly parabolic pattern. This systematic behavior of the negative-parity states suggests a moderate evolution of octupole collectivity in the neutron-rich lanthanide region. However, when compared to experimental data, the predicted negative-parity bands for Ba and Xe isotopes consistently exhibit elongation. The underlying reason for this observation is the same as that discussed for the positive-parity states depicted in Figure 1. 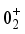 ,
, 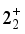 , and
, and 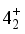 levels. These states appear to form a quasi-beta band, where the 0 state acts as the bandhead for nuclei with N > 90. Notably, the computed energy levels exhibit an unconventional pattern for transitional nuclei with N < 90, as illustrated in Figure 3. In particular, the positions of the
levels. These states appear to form a quasi-beta band, where the 0 state acts as the bandhead for nuclei with N > 90. Notably, the computed energy levels exhibit an unconventional pattern for transitional nuclei with N < 90, as illustrated in Figure 3. In particular, the positions of the 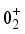 and
and 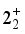 and energy levels are reversed, leading to an uneven band structure. This inversion results in significant level repulsion between low-spin states. Moreover, as depicted in Figures (3c) and (3d) for the highly quadrupole-deformed Ce and Nd isotopes, respectively, the calculated energy levels differ significantly from the observed ones. This discrepancy is a common characteristic of mapped IBM studies, primarily due to the unexpectedly high value of
and energy levels are reversed, leading to an uneven band structure. This inversion results in significant level repulsion between low-spin states. Moreover, as depicted in Figures (3c) and (3d) for the highly quadrupole-deformed Ce and Nd isotopes, respectively, the calculated energy levels differ significantly from the observed ones. This discrepancy is a common characteristic of mapped IBM studies, primarily due to the unexpectedly high value of 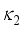 observed ones. Indeed, this discrepancy between the calculated and observed energy levels is a common characteristic of mapped IBM research, primarily attributed to the unexpectedly high value of
observed ones. Indeed, this discrepancy between the calculated and observed energy levels is a common characteristic of mapped IBM research, primarily attributed to the unexpectedly high value of 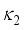 . Indeed, this discrepancy between the calculated and observed energy levels is a common characteristic of mapped IBM research, primarily attributed to the unexpectedly high value of
. Indeed, this discrepancy between the calculated and observed energy levels is a common characteristic of mapped IBM research, primarily attributed to the unexpectedly high value of 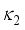 .
. 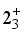 ,
, 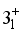 ,
, 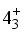 and
and 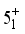 levels. According to the current calculations, these states are found to be associated with quasi-γ bands in the majority of the studied nuclei. As depicted in Figure 4, the energy levels exhibit a nearly harmonic pattern. However, it is worth noting that the
levels. According to the current calculations, these states are found to be associated with quasi-γ bands in the majority of the studied nuclei. As depicted in Figure 4, the energy levels exhibit a nearly harmonic pattern. However, it is worth noting that the 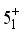 level stands out with a notably higher energy compared to the other levels in the band. This is especially prominent for lighter isotopes with lower neutron numbers. The experimental bandhead energy of the quasi-gamma band is significantly overestimated for the same reason as the quasi-beta band. In Figure 5, the expectation value of the f-boson number operator, derived from the IBM wave functions of the states (a)
level stands out with a notably higher energy compared to the other levels in the band. This is especially prominent for lighter isotopes with lower neutron numbers. The experimental bandhead energy of the quasi-gamma band is significantly overestimated for the same reason as the quasi-beta band. In Figure 5, the expectation value of the f-boson number operator, derived from the IBM wave functions of the states (a)  , (b)
, (b) 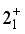 , (c)
, (c) 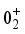 , (d)
, (d) 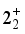 , (e)
, (e) 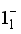 , and (f)
, and (f) 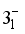 , is plotted.
, is plotted. 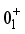 and
and  states exhibit a substantial presence of f-boson components (
states exhibit a substantial presence of f-boson components (  ) at N ≈ 88. This suggests that, for nuclei with N ≈ 88, the octupole degree of freedom plays a vital role in shaping the low spin structure of the positive-parity ground-state bands.
) at N ≈ 88. This suggests that, for nuclei with N ≈ 88, the octupole degree of freedom plays a vital role in shaping the low spin structure of the positive-parity ground-state bands. 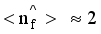 condition holds, indicating that the 0 state possesses a double octupole boson nature. Specifically, for
condition holds, indicating that the 0 state possesses a double octupole boson nature. Specifically, for  , the f-boson content of the
, the f-boson content of the  state is comparable to that of the
state is comparable to that of the 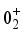 state. Additionally, the wave functions of the
state. Additionally, the wave functions of the 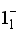 and
and  states exhibit f bosons within the
states exhibit f bosons within the  range.
range. 3.2. Electric Transition Probability
 are used to calculate transition probabilities. They are defined as follows
are used to calculate transition probabilities. They are defined as follows  (5)
(5) 
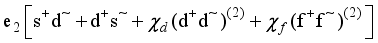 (6)
(6) 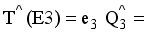
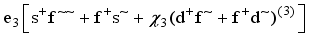 (7)
(7) 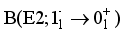 and
and 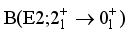 transition probabilities, the boson effective charges e1 = 0.02
transition probabilities, the boson effective charges e1 = 0.02  and e2 = 0.17
and e2 = 0.17  are fixed. Nonetheless, the significant
are fixed. Nonetheless, the significant  values seen experimentally in those nuclei with elevated octupole correlations must be taken into account in order to fix e3.
values seen experimentally in those nuclei with elevated octupole correlations must be taken into account in order to fix e3. 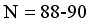 , they exhibit a sharp increase that is compatible with the emergence of substantial collectivity. Furthermore, N = 88 corresponds to the maximum B(E3) rate for each isotopic chain. Additionally, there is a fair amount of agreement between the computed and experimental B(E3) values. Specifically, the estimated B(E3) rates for 144,146Ba fall within the experimental error ranges
, they exhibit a sharp increase that is compatible with the emergence of substantial collectivity. Furthermore, N = 88 corresponds to the maximum B(E3) rate for each isotopic chain. Additionally, there is a fair amount of agreement between the computed and experimental B(E3) values. Specifically, the estimated B(E3) rates for 144,146Ba fall within the experimental error ranges Nuclei | Eλ | transitions | Exp. | IBM-1 |
|---|---|---|---|---|
144Ba | E2 | 42 | ||
78 | ||||
52 | ||||
55.5 | ||||
E3 | 51 | |||
90 | ||||
121 | ||||
146Ba | E1 | 11 | ||
6.2 | ||||
1.88 | ||||
1.96 | ||||
E2 | 67 | |||
102 | ||||
89 | ||||
59 | ||||
48 | ||||
E3 | 55 | |||
70 | ||||
80 | ||||
102 | ||||
148Nd | E1 | 0.030 | ||
0.055 | ||||
0.043 | ||||
E2 | 53.8 | |||
98.3 | ||||
33.0 | ||||
0.62 | ||||
16.2 | ||||
18 | ||||
2.72 | ||||
105 | ||||
E3 |
 and
and  states in Xe and Ba isotopes. This can be attributed to the occupancy of f7/2 (g7/2) orbitals by neutrons (protons) in this region, which form nucleon pairs with J = 6+. The inclusion of the equivalent
states in Xe and Ba isotopes. This can be attributed to the occupancy of f7/2 (g7/2) orbitals by neutrons (protons) in this region, which form nucleon pairs with J = 6+. The inclusion of the equivalent  boson in the IBM framework may lead to a lowering of the energy of these yrast states with
boson in the IBM framework may lead to a lowering of the energy of these yrast states with  , providing a more accurate description of their spectroscopic properties.
, providing a more accurate description of their spectroscopic properties. 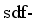 IBM framework. Performing such calculations can provide a more comprehensive understanding of the underlying physics and help bridge the gap between experimental observations and theoretical predictions for the 7− state in these isotopes.
IBM framework. Performing such calculations can provide a more comprehensive understanding of the underlying physics and help bridge the gap between experimental observations and theoretical predictions for the 7− state in these isotopes.  energy in Ba and Nd isotopes, as evidenced by the results. To further explore this phenomenon, it would be valuable to investigate whether the empirical trend of this state can be replicated using fermionic calculations within the
energy in Ba and Nd isotopes, as evidenced by the results. To further explore this phenomenon, it would be valuable to investigate whether the empirical trend of this state can be replicated using fermionic calculations within the 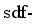 IBM framework. By employing fermionic calculations, researchers can delve deeper into the underlying physics and determine if incorporating additional fermionic degrees of freedom can better capture the observed empirical trend of the
IBM framework. By employing fermionic calculations, researchers can delve deeper into the underlying physics and determine if incorporating additional fermionic degrees of freedom can better capture the observed empirical trend of the  state in Ba and Nd isotopes. This investigation can provide valuable insights into the nuclear structure and shed light on the interplay between collective and single-particle degrees of freedom.
state in Ba and Nd isotopes. This investigation can provide valuable insights into the nuclear structure and shed light on the interplay between collective and single-particle degrees of freedom. | [1] | P. A. Butler and W. Nazarewicz, Rev. Mod. Phys. 68 (1996) 349. |
| [2] | P. A. Butler, J. Phys. G: Nucl. Part. Phys. 43 (2016) 073002. |
| [3] | P. A. Butler, Proc. Roy. Soc. A: Mathematical, Physical and Engineering Sciences 476 (2020) 0200202. |
| [4] | L. P. Gaffney, P. A. Butler, M. Scheck, A. B. Hayes, F. Wenander, M. Albers, B. Bastin, C. Bauer, A. Blazhev, S. B¨onig, N. Bree, J. Cederk¨all, T. Chupp, D. Cline, T. E. Cocolios, T. Davinson, H. D. Witte, J. Diriken, T. Grahn, A. Herzan, M. Huyse, D. G. Jenkins, D. T. Joss, N. Kesteloot, J. Konki, M. Kowalczyk, T. Kr¨oll, E. Kwan, R. Lutter, K. Moschner, P. Napiorkowski, J. Pakarinen, M. Pfeiffer, D. Radeck, P. Reiter, K. Reynders, S. V. Rigby, L. M. Robledo, M. Rudigier, S. Sambi, M. Seidlitz, B. Siebeck, T. Stora, P. Thoele, P. V. Duppen, M. J. Vermeulen, M. von Schmid, D. Voulot, N. Warr, K. Wimmer, K. WrzosekLipska, C. Y. Wu, and M. Zielinska, Nature (London) 497 (2013) 199. |
| [5] | B. Bucher, S. Zhu, C. Y. Wu, R. V. F. Janssens, D. Cline, A. B. Hayes, M. Albers, A. D. Ayangeakaa, P. A. Butler, C. M. Campbell, M. P. Carpenter, C. J. Chiara, J. A. Clark, H. L. Crawford, M. Cromaz, H. M. David, C. Dickerson, E. T. Gregor, J. Harker, C. R. Hoffman, B. P. Kay, F. G. Kondev, A. Korichi, T. Lauritsen, A. O. Macchiavelli, R. C. Pardo, A. Richard, M. A. Riley, G. Savard, M. Scheck, D. Seweryniak, M. K. Smith, R. Vondrasek, and A. Wiens, Phys. Rev. Lett. 116 (2016) 112503. |
| [6] | B. Bucher, S. Zhu, C. Y. Wu, R. V. F. Janssens, R. N. Bernard, L. M. Robledo, T. R. Rodr´ıguez, D. Cline, A. B. Hayes, A. D. Ayangeakaa, M. Q. Buckner, C. M. Campbell, M. P. Carpenter, J. A. Clark, H. L. Crawford, H. M. David, C. Dickerson, J. Harker, C. R. Hoffman, B. P. Kay, F. G. Kondev, T. Lauritsen, A. O. Macchiavelli, R. C. Pardo, G. Savard, D. Seweryniak, and R. Vondrasek, Phys. Rev. Lett. 118 (2017) 152504. |
| [7] | P. A. Butler, L. P. Gaffney, P. Spagnoletti, K. Abrahams, M. Bowry, J. Cederk¨all, G. de Angelis, H. De Witte, P. E. Garrett, A. Goldkuhle, C. Henrich, A. Illana, K. Johnston, D. T. Joss, J. M. Keatings, N. A. Kelly, M. Komorowska, J. Konki, T. Kroll, M. Lozano, B. S. Nara Singh, D. O’Donnell, J. Ojala, R. D. Page, L. G. Pedersen, C. Raison, P. Reiter, J. A. Rodriguez, D. Rosiak, S. Rothe, M. Scheck, M. Seidlitz, T. M. Shneidman, B. Siebeck, J. Sinclair, J. F. Smith, M. Stryjczyk, P. Van Duppen, S. Vinals, V. Virtanen, N. Warr, K. Wrzosek-Lipska, and M. Zieli´nska, Phys. Rev. Lett. 124 (2020) 042503. |
| [8] | M. M. R. Chishti, D. O’Donnell, G. Battaglia, M. Bowry, D. A. Jaroszynski, B. S. N. Singh, M. Scheck, P. Spagnoletti, and J. F. Smith, Nat. Phys. 16 (2022) 853. |
| [9] | D. Bonatsos, D. Lenis, N. Minkov, D. Petrellis, and P. Yotov, Phys. Rev. C 71 (2023) 064309. |
| [10] | P. G. Bizzeti and A. M. Bizzeti-Sona, Phys. Rev. C 88 (2013) 011305. |
| [11] | N. Yoshinaga, K. Yanase, K. Higashiyama and E. Teruya, Phys. Rev. C 98 (2018) 044321. |
| [12] | N. Yoshinaga, K. Yanase, C. Watanabe, and K. Higashiyama, Prog. Theor. Exp. Phys. 221 (2021) 063D01. |
| [13] | O. Vallejos and J. Barea, Phys. Rev. C 104 (2021) 014308. |
| [14] | T. M. Shneidman, G. G. Adamian, N. V. Antonenko, R. V. Jolos, and W. Scheid, Phys. Lett. B 526 (2002) 322. |
| [15] | T. M. Shneidman, G. G. Adamian, N. V. Antonenko, R. V. Jolos, and W. Scheid, Phys. Rev. C 67 (203) 014313. |
| [16] | P. Ring and P. Schuck, The nuclear many-body problem, (Berlin: Springer-Verlag, 1980). |
| [17] | R. Lic˘a, G. Benzoni, T. R. Rodr´ıguez, M. J. G. Borge, L. M. Fraile, H. Mach, A. I. Morales, M. Madurga, C. O. Sotty, V. Vedia, H. De Witte, J. Benito, R. N. Bernard, T. Berry, A. Bracco, F. Camera, S. Ceruti, V. Charviakova, N. Cieplicka-Ory´nczak, C. Costache, F. C. L. Crespi, J. Creswell, G. Fernandez-Mart´ınez, H. Fynbo, P. T. Greenlees, I. Homm, M. Huyse, J. Jolie, V. Karayonchev, U. K¨oster, J. Konki, T. Kroll, J. Kurcewicz, T. Kurtukian-Nieto, I. Lazarus, M. V. Lund, N. M˘arginean, R. M˘arginean, C. Mihai, R. E. Mihai, A. Negret, A. Orduz, Z. Patyk, S. Pascu, V. Pucknell, P. Rahkila, E. Rapisarda, J. M. Regis, L. M. Robledo, F. Rotaru, N. Saed-Samii, V. S´anchez-Tembleque, M. Stanoiu, O. Tengblad, M. Thuerauf, A. Turturica, P. Van Duppen, and N. Warr (IDS Collaboration), Phys. Rev. C 97 (2018) 024305. |
| [18] | Y. Fu, H. Wang, L.-J. Wang, and J. M. Yao, Phys. Rev. C 97 (2018) 024338. |
| [19] | L. M. Robledo and P. A. Butler, Phys. Rev. C 88 (2013) 051302. |
| [20] | L. M. Robledo, J. L. Egido, B. Nerlo-Pomorska, and K. Pomorski, Phys. Lett. B 201 (1998) 409. |
| [21] | S. Y. Xia, H. Tao, Y. Lu, Z. P. Li, T. Nikˇsi´c, and D. Vretenar, Phys. Rev. C 96, 054303 (2017). |
| [22] | K. Nomura, L. Lotina, T. Niksic, and D. Vretenar, Phys. Rev. C 103 (2021), 054301. |
| [23] | T. Otsuka, A. Arima, and F. Iachello, Nucl. Phys. A 309 (1978) 1. |
| [24] | T. Mizusaki and T. Otsuka, Prog. Theor. Phys. Suppl. 125 (1996) 97. |
| [25] | K. Nomura, R. Rodr´ıguez-Guzm´an, Y. M. Humadi, L. M. Robledo, and J. E. Garc´ıa-Ramos, Phys. Rev. C 102 (2020) 064326. |
| [26] | K. Nomura, R. Rodr´ıguez-Guzm´an, L. M. Robledo, and J. E. Garc´ıa-Ramos, Phys. Rev. C 103 (2021) 044311. |
| [27] | K. Nomura, R. Rodr´ıguez-Guzm´an, and L. M. Robledo, Phys. Rev. C 92 (2015) 014312. |
| [28] | Brookhaven National Nuclear Data Center, |
| [29] | M. Sugawara and H. Kusakari, Phys. Rev. C 75, 067302 (2007). |
| [30] | J. B. Gupta and M. Saxena, Phys. Rev. C 91, 054312 (2015). |
| [31] | S. Y. Lee, J. H. Lee, and Y. J. Lee, J. Korean Phys. Soc. 72, 1147 (2018). |
| [32] | S. J. Zhu, E. H. Wang, J. H. Hamilton, A. V. Ramayya, Y. X. Liu, N. T. Brewer, Y. X. Luo, J. O. Rasmussen, Z. G. Xiao, Y. Huang, G. M. Ter-Akopian, and T. Oganessian, Phys. Rev. Lett. 124 (2020) 032501. |
| [33] | T. Kibedi and R. Spear, Atomic Data and Nuclear Data Tables 80 (2002) 35. |
APA Style
Hashim, T. A., Abood, S. N. (2024). Study of Octupole Transitions in Xe, Ba, Ce and Nd Nuclei within Interacting Boson Model. American Journal of Modern Energy, 10(2), 18-24. https://doi.org/10.11648/j.ajme.20241002.11
ACS Style
Hashim, T. A.; Abood, S. N. Study of Octupole Transitions in Xe, Ba, Ce and Nd Nuclei within Interacting Boson Model. Am. J. Mod. Energy 2024, 10(2), 18-24. doi: 10.11648/j.ajme.20241002.11
AMA Style
Hashim TA, Abood SN. Study of Octupole Transitions in Xe, Ba, Ce and Nd Nuclei within Interacting Boson Model. Am J Mod Energy. 2024;10(2):18-24. doi: 10.11648/j.ajme.20241002.11
@article{10.11648/j.ajme.20241002.11,
author = {Tuqa Abdulbaset Hashim and Saad Naji Abood},
title = {Study of Octupole Transitions in Xe, Ba, Ce and Nd Nuclei within Interacting Boson Model
},
journal = {American Journal of Modern Energy},
volume = {10},
number = {2},
pages = {18-24},
doi = {10.11648/j.ajme.20241002.11},
url = {https://doi.org/10.11648/j.ajme.20241002.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajme.20241002.11},
abstract = {For nuclei with 54≤Z≤60 and 86≤N≤94, the results regarding the excitation spectra at low energies, both in positive and negative parity, as well as the transition probabilities for electric dipole (B(E1)), quadrupole (B(E2)), and octupole transitions (B(E(3)), indicate the emergence of significant octupole behavior. These observations have been made using the Interacting Boson Model-1 (IBM-1). The study examines the onset of octupole deformation and its impact on the spectroscopic characteristics in even-even neutron-rich lanthanide isotopes, specifically in the Ba and Nd nuclei. The investigation compares the results obtained from the Interacting Boson Model-1 (IBM-1) with the existing experimental data. The focus is on understanding how the addition of neutrons influences the development of octupole deformation and its manifestation in the observed spectroscopic features. The onset of strong octupolarity for Z≈ 56 and N ≈ 88 nuclei is indicated by the results obtained for the electric dipole, quadrupole, and octupole transition probabilities, as well as the low-energy positive and negative-parity excitation spectra. Conversely, discrepancies between the spectroscopic data and the IBM results suggest that the mapping quality needs to be evaluated in order to determine if the mapped boson Hamiltonian or the fermionic calculations are the source of the issues.
},
year = {2024}
}
TY - JOUR T1 - Study of Octupole Transitions in Xe, Ba, Ce and Nd Nuclei within Interacting Boson Model AU - Tuqa Abdulbaset Hashim AU - Saad Naji Abood Y1 - 2024/04/28 PY - 2024 N1 - https://doi.org/10.11648/j.ajme.20241002.11 DO - 10.11648/j.ajme.20241002.11 T2 - American Journal of Modern Energy JF - American Journal of Modern Energy JO - American Journal of Modern Energy SP - 18 EP - 24 PB - Science Publishing Group SN - 2575-3797 UR - https://doi.org/10.11648/j.ajme.20241002.11 AB - For nuclei with 54≤Z≤60 and 86≤N≤94, the results regarding the excitation spectra at low energies, both in positive and negative parity, as well as the transition probabilities for electric dipole (B(E1)), quadrupole (B(E2)), and octupole transitions (B(E(3)), indicate the emergence of significant octupole behavior. These observations have been made using the Interacting Boson Model-1 (IBM-1). The study examines the onset of octupole deformation and its impact on the spectroscopic characteristics in even-even neutron-rich lanthanide isotopes, specifically in the Ba and Nd nuclei. The investigation compares the results obtained from the Interacting Boson Model-1 (IBM-1) with the existing experimental data. The focus is on understanding how the addition of neutrons influences the development of octupole deformation and its manifestation in the observed spectroscopic features. The onset of strong octupolarity for Z≈ 56 and N ≈ 88 nuclei is indicated by the results obtained for the electric dipole, quadrupole, and octupole transition probabilities, as well as the low-energy positive and negative-parity excitation spectra. Conversely, discrepancies between the spectroscopic data and the IBM results suggest that the mapping quality needs to be evaluated in order to determine if the mapped boson Hamiltonian or the fermionic calculations are the source of the issues. VL - 10 IS - 2 ER -