This work concerns the calculations of interacting boson fermion-fermion model (IBFFM) for the odd-odd nucleus 134Cs. The energy levels (positive and negative parity states), electric transition probability B(E2), magnetic transition probability B(M1), quadrupole and magnetic dipole moments have been studied in this work. The IBFFM results are compared with the available experimental data. In the present work, the IBFFM pattern of total and parametric dependent level densities for the odd-odd nucleus 134Cs is investigated and compared to the pattern found in previous investigations in the framework of combinatorial and spectral distribution approaches. When comparing the theoretical values with the available experimental values, it was found that there is a good match between them. This is due to the values of the Hamiltonian parameters that were found accurately, so this IBFFM model is considered one of the effective models in studying the nuclear structure of odd-odd nuclei. The level density of the odd-odd nucleus 196Au is investigated in the interacting boson-fermion-fermion model (IBFFM) which accounts for collectivity and complex interaction between quasiparticle and collective modes. The IBFFM spin-dependent level densities show high-spin reduction with respect to Bethe formula. This can be well accounted for by a modified spin-dependent level density formula.
| Published in | American Journal of Modern Energy (Volume 10, Issue 1) |
| DOI | 10.11648/j.ajme.20241001.12 |
| Page(s) | 11-17 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
IBFFM, Energy Levels, Electromagnetic Transitions
 , which has been the subject of intensive experimental investigation
, which has been the subject of intensive experimental investigation 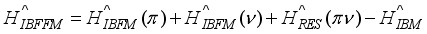 (1)
(1) 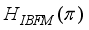 and
and 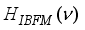
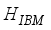
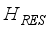 stands for the residual proton-neutron interaction. The IBFFM code includes the residual interactions spin-spin, multipole-multipole, spin-spin-delta, and tensor interaction, which are represented by the study of Paar et al.,
stands for the residual proton-neutron interaction. The IBFFM code includes the residual interactions spin-spin, multipole-multipole, spin-spin-delta, and tensor interaction, which are represented by the study of Paar et al., 
 (2)
(2) 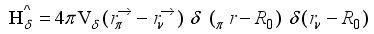 (3)
(3) 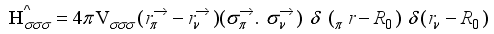 (4)
(4) 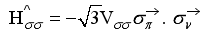 (5)
(5)  (6)
(6) 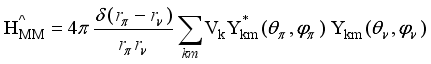 (7)
(7) 
 (8)
(8) 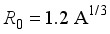 , the parameters
, the parameters  and
and  are constants, and determined the strengths of the interactions.
are constants, and determined the strengths of the interactions. 3.1. Energy Spectra
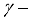 dependence on the potential energy surface, in qualitative accord with earlier computations for
dependence on the potential energy surface, in qualitative accord with earlier computations for  ,
,  even-even nuclei carried out in the classic collective model
even-even nuclei carried out in the classic collective model 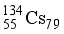 , the four lowest-lying positive-party levels are 4+, 5+, 3+, and the state at 0.174 MeV, which is designated as 2+ or 3+. In the
, the four lowest-lying positive-party levels are 4+, 5+, 3+, and the state at 0.174 MeV, which is designated as 2+ or 3+. In the  reaction, these states are significantly stimulated by
reaction, these states are significantly stimulated by 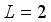 transfer, and in the (t,
transfer, and in the (t, 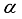 ) reaction, by
) reaction, by  transfer. Assuming these four levels contain sizable components with (
transfer. Assuming these four levels contain sizable components with (  and the 2+ member of the (
and the 2+ member of the ( 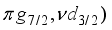 multiplets, this is consistent with the (
multiplets, this is consistent with the (  assumption
assumption 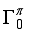 ,
, 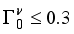 ,
, 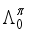 ,
, 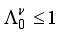 ), the estimated quadrupole moment of the 4+ ground state has a negative sign, which is in contradiction with experiment
), the estimated quadrupole moment of the 4+ ground state has a negative sign, which is in contradiction with experiment 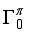 ,
, 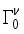 ,
,  ,
, 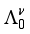 ) that this pattern is comparatively stable within that range of values. However, it is important to notice that for
) that this pattern is comparatively stable within that range of values. However, it is important to notice that for 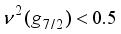 , this pattern is consistent with the parabolic rule
, this pattern is consistent with the parabolic rule  ,
, 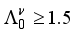 , the states 4+, 5+, 3+, and 2+ (lie on a parabola) open up and become the domain of parametrization for which we can obtain the experimentally observed pattern, with the 4+ state acting as the ground state with positive quadrupole moment. Table 1 displays the calculated positive-parity levels of 134Cs up to 0.300 MeV.
, the states 4+, 5+, 3+, and 2+ (lie on a parabola) open up and become the domain of parametrization for which we can obtain the experimentally observed pattern, with the 4+ state acting as the ground state with positive quadrupole moment. Table 1 displays the calculated positive-parity levels of 134Cs up to 0.300 MeV. 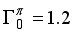 MeV,
MeV, 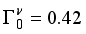 MeV,
MeV,  MeV,
MeV, 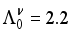 MeV,
MeV, 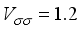 MeV,
MeV, 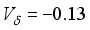 MeV. The 4+, 5+, 3+, and 2+ states wave functions are dominated by components that have
MeV. The 4+, 5+, 3+, and 2+ states wave functions are dominated by components that have 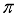 g7/2 and
g7/2 and  5/2 configurations.
5/2 configurations. 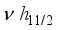 , the quasiparticle with negative panty, additionally, we have determined the occupation probability for negative-parity states using Kisslinger-Sorensen (v2=0.850), attempting to replicate the intricate experimental pattern that would indicate a deformed parabola opening up.
, the quasiparticle with negative panty, additionally, we have determined the occupation probability for negative-parity states using Kisslinger-Sorensen (v2=0.850), attempting to replicate the intricate experimental pattern that would indicate a deformed parabola opening up. 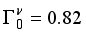 MeV,
MeV,  MeV, we utilize the same boson-fermion parametrization as for the positive-parity states to get the negative-parity levels depicted in Table 1 up to 0.600 MeV.
MeV, we utilize the same boson-fermion parametrization as for the positive-parity states to get the negative-parity levels depicted in Table 1 up to 0.600 MeV. Positive parity states | Negative parity states | ||||
|---|---|---|---|---|---|
Levels | Exp. [24] | IBFFM | Levels | Exp. [24] | IBFFM |
0.0 | 0.0 | 0.138 | 0.142 | ||
0.0112 | 0.010 | 0.1764 | 0.170 | ||
0.0600 | 0.077 | 0.193 | 0.211 | ||
0.173 | 0.167 | 0.257 | 0.289 | ||
0.176 | 0.180 | 0.267 | 0.271 | ||
0.190 | 0.195 | 0.344 | 0.376 | ||
0.197 | 0210 | 0.382 | 0.391 | ||
0.209 | 0.218 | 0.434 | 0.442 | ||
0.234 | 0.239 | 0.450 | 0.481 | ||
0.274 | 0.281 | 0.483 | 0.510 | ||
0.290 | 0.301 | 0.570 | 0.589 | ||
0.377 | 0.367 | 0.613 | 0.633 | ||
0.451 | 0.433 | 0.624 | 0.645 | ||
0.454 | 0.476 | 0.643 | 0.681 | ||
0.502 | 0.511 | 0.684 | 0.697 | ||
0.519 | 0.522 | 0.701 | 0.721 | ||
0.539 | 0.559 | 0.715 | 0.20 | ||
0.579 | 0.588 | 0.752 | 0.755 | ||
0.584 | 0.611 | 0.783 | 0.792 | ||
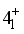 state wave function, which was produced by diagonalizing HIBFFM in basis
state wave function, which was produced by diagonalizing HIBFFM in basis 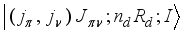 , has the following biggest components (see Table 2):
, has the following biggest components (see Table 2): levels | Wavefunction components |
|---|---|
0.593 |
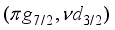 . even if the wave functions are more complicated, 2+, 3+, 4+, 5+, and
. even if the wave functions are more complicated, 2+, 3+, 4+, 5+, and 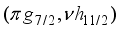
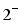 ,
, 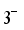 ,...,
,..., 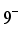 . Furthermore, many characteristics of these states can be roughly explained within the context of the zeroth-order classification and the simple parabolic rule
. Furthermore, many characteristics of these states can be roughly explained within the context of the zeroth-order classification and the simple parabolic rule 3.2. Electromagnetic Properties
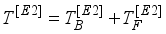 (9)
(9) 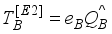 (10)
(10) 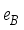 is the boson effective charge in (e. b) units and
is the boson effective charge in (e. b) units and  stands for the quadrupole operator is takes by
stands for the quadrupole operator is takes by  (11)
(11) 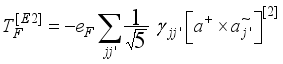 (12)
(12)  standing for the effective fermion charge,
standing for the effective fermion charge, 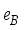 is fitted to reproduced the experimental
is fitted to reproduced the experimental  value of the corresponding even-even boson-core nuclei, as in earlier research
value of the corresponding even-even boson-core nuclei, as in earlier research  is assumed to be equal to
is assumed to be equal to  for all the investigated odd-mass nuclei. The quadrupole moments equation is given by
for all the investigated odd-mass nuclei. The quadrupole moments equation is given by  (13)
(13) 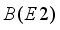 value is given as
value is given as  (14)
(14) 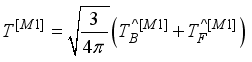 (15)
(15) 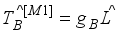 with the gyro-magnetic factor
with the gyro-magnetic factor 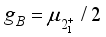 given in terms of the magnetic moment
given in terms of the magnetic moment 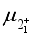 of the
of the  state of the even-even nucleus. The M1 operator for fermion part is given by
state of the even-even nucleus. The M1 operator for fermion part is given by  (16)
(16) 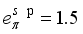 and
and  , respectively, whereas the boson charge,
, respectively, whereas the boson charge, 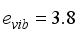 , is aligned with the 4+ state electric quadrupole moment. For medium-heavy nuclei, the boson charges range (
, is aligned with the 4+ state electric quadrupole moment. For medium-heavy nuclei, the boson charges range ( 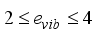 ) that was formerly employed is qualitatively consistent with this result. According to conventional values, the ratios of gyromagnets are
) that was formerly employed is qualitatively consistent with this result. According to conventional values, the ratios of gyromagnets are 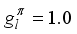 ,
,  ,
,  ,
, 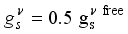 ,
, 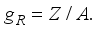 . The concordance between the measured and estimated magnetic moment of the ground state is improved by a little decrease in
. The concordance between the measured and estimated magnetic moment of the ground state is improved by a little decrease in  . The table illustrates how successfully the g-values that were used to simulate the magnetic dipole moments of states 5+ and
. The table illustrates how successfully the g-values that were used to simulate the magnetic dipole moments of states 5+ and  .
. 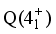 . Upon nearer examination, the off-diagonal boson contributions of
. Upon nearer examination, the off-diagonal boson contributions of 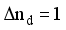 are responsible for the major partial contributions to
are responsible for the major partial contributions to 
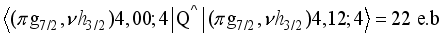
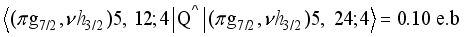
levels | Q(e.b). | μ(μN) | ||
|---|---|---|---|---|
Exp. [24] | IBFFM | Exp. [24] | IBFFM | |
0.39 | 0.389 | 2.99 | 2.83 | |
- | 0.044 | 2.33 | 3.33 | |
- | -0.55 | - | 2.40 | |
- | -0.39 | - | 1.99 | |
- | 1.33 | 1.10 | 1.18 | |
- | 0.97 | - | -1.99 | |
- | 0.71 | - | -0.98 | |
- | 0.55 | - | 0.47 | |
- | 0.45 | - | -0.24 | |
- | 1.32 | - | 0.89 | |
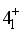 state wave function.
state wave function. 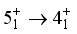 transitions that have been calculated are:
transitions that have been calculated are: 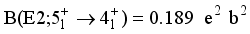 ,
, 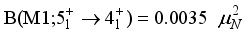
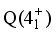 and the high value of B(E2). The partial contributions incoherence is the cause of
and the high value of B(E2). The partial contributions incoherence is the cause of 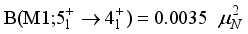 decrease.
decrease.  state half-life,
state half-life, 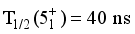 , is obtained by tabulating internal conversion coefficients and using the computed B (M 1) and B(E2) values for the
, is obtained by tabulating internal conversion coefficients and using the computed B (M 1) and B(E2) values for the 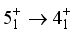 transition. This is in reasonable with experimental data of 45 ns.
transition. This is in reasonable with experimental data of 45 ns. 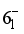 state
state  using the experimental branching ratio
using the experimental branching ratio 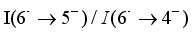 and the calculated internal conversion constants, this corresponds reasonably well with the experimental measurement of 12 ns. These values are calculated for the
and the calculated internal conversion constants, this corresponds reasonably well with the experimental measurement of 12 ns. These values are calculated for the 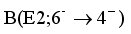 and
and  transitions. As a result, the distribution of boson charges found from matches the available lifetimes
transitions. As a result, the distribution of boson charges found from matches the available lifetimes transitions | Excitation Energy (MeV) | ||
|---|---|---|---|
Exp. | IBFFM | ||
0.112 | 1 | 1 | |
0.060 | 1 | 0.06 | |
0.048 | 0.03 | ||
1.139 | 1 | 0.18 | |
1.738 | 0.01 | 1 | |
0.173 | 1 | 1 | |
0.741 | 1 | 0.9 | |
0.106 | - | 0.10 | |
0.931 | - | 0.008 | |
1.184 | 1 | 1 | |
0.653 | 0.03 | 0.061 | |
2.056 | 1 | 0.92 | |
0.873 | 0.23 | 0.29 | |
0.767 | - | 0.009 | |
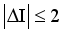 ,
, 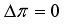 have the strongest branches at
have the strongest branches at 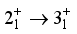 ,
,  ,
, 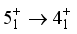 and
and 
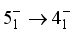 ,
,  respectively. The majority of the
respectively. The majority of the 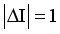 transitions are M1 type, which is consistent with experimental results.
transitions are M1 type, which is consistent with experimental results. 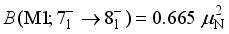 ,
,  .
. | [1] | V. M. Alexcev, Nucl. Phys. A 297 (1978) 373. |
| [2] | F. Ackerman, E. W. Otten, G. zu Pulitz, A. Schenck and S. Ultrich, Nucl. Phys. A248 (1975) 157. |
| [3] | M. Bogdanovic, Nucl. Phys. A 249 (1976) 120. |
| [4] | A. Arima and F. Iachello, Phys. Rev. Lett. 35 (1975) 1069. |
| [5] | F. Iachello and O. Scholten, Phys. Rev. Lett. 43 (1979) 679. |
| [6] | S. Brant, V. Paar and D. Vertenar, Z. Phys. A 319 (1984) 335. |
| [7] | V. Paar, "Capture gamma ray spectroscopy and related topics" ed. S. Raman, American Institute of Physics, New York 1985. |
| [8] | T. Hubsch and V. Paar, Z. Phys. A 319 (2018) 111. |
| [9] | P. Van Isacker, J. Jolie, K. Heyde and A. Frank, Phys. Lett. 54 (1985) 653. |
| [10] | A. B. Balantekin and V. Paar, Phys. Lett. 54 (2022) 9. |
| [11] | A. A. Hammood and S. N. Abood "AIP Conference Proceeding" current Issue. Vol. 3040, isuue 1 (2023). |
| [12] | D. Vretenar, S. Brant and V. Paar, "Computer code IBFFM" IKP Julich (1985). |
| [13] | N. Amiri, M. Ghapanvari, M. A. Jafarizadeh and S. Vosoughi, Nucl. Phys. A 1002 (2020) 121961. |
| [14] | J. Ragnarsson, A. Sibiczewski, R. K. Sheline, S. E. Larsson and B. Nrelo-Pomorska, Nucl. Phys. A233 (1974) 329. |
| [15] | G. Gneuss and W. Grener, Nucl. Phys. A 171 (1971) 449. |
| [16] | D. Habs, H. Klewe-Nebenius, K. Wisshak, R. Lohken, G. Nowicki and H. Rebel, Z. Phys. 267 (2022) 149. |
| [17] | O. Scholten Ph. D Thesis, University of Groningen 1980. |
| [18] | V. Paar, S. Barant, L. F. Canto, G. Leander and M. Vouk, Nucl. Phys. A 378 (2009) 41. |
| [19] | L. S. Kisslinger and R. A. Sorensen, Rev. Mod. Phys. 35 (1963) 853. |
| [20] | J. Timar, T. Fenyes, T. Kibedi, A. Passoja, M. Luontana, W. Trzaska ana V. Paar, Nucl. Phys. A 455 (1986) 477. |
| [21] | V. Paar, Nucl. Phys. A 331 (1979) 16. |
| [22] | B. H. Wildenthal, Phys. Rev. C3 (2021) 1199. |
| [23] | S. Brant and D. Tonev, J. Phys.: Conf. Ser. 205 (2022) 012026. |
| [24] | A. A. Sonzogni, Nucl. Data Sheets 103 (2004) 112. |
APA Style
Mohaisen, A. J., Abood, S. N. (2024). An Application of Interacting Boson Fermion-Fermion Model (IBFFM) for 134Cs Nucleus. American Journal of Modern Energy, 10(1), 11-17. https://doi.org/10.11648/j.ajme.20241001.12
ACS Style
Mohaisen, A. J.; Abood, S. N. An Application of Interacting Boson Fermion-Fermion Model (IBFFM) for 134Cs Nucleus. Am. J. Mod. Energy 2024, 10(1), 11-17. doi: 10.11648/j.ajme.20241001.12
AMA Style
Mohaisen AJ, Abood SN. An Application of Interacting Boson Fermion-Fermion Model (IBFFM) for 134Cs Nucleus. Am J Mod Energy. 2024;10(1):11-17. doi: 10.11648/j.ajme.20241001.12
@article{10.11648/j.ajme.20241001.12,
author = {Afrah Jawad Mohaisen and Saad Naji Abood},
title = {An Application of Interacting Boson Fermion-Fermion Model (IBFFM) for 134Cs Nucleus
},
journal = {American Journal of Modern Energy},
volume = {10},
number = {1},
pages = {11-17},
doi = {10.11648/j.ajme.20241001.12},
url = {https://doi.org/10.11648/j.ajme.20241001.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajme.20241001.12},
abstract = {This work concerns the calculations of interacting boson fermion-fermion model (IBFFM) for the odd-odd nucleus 134Cs. The energy levels (positive and negative parity states), electric transition probability B(E2), magnetic transition probability B(M1), quadrupole and magnetic dipole moments have been studied in this work. The IBFFM results are compared with the available experimental data. In the present work, the IBFFM pattern of total and parametric dependent level densities for the odd-odd nucleus 134Cs is investigated and compared to the pattern found in previous investigations in the framework of combinatorial and spectral distribution approaches. When comparing the theoretical values with the available experimental values, it was found that there is a good match between them. This is due to the values of the Hamiltonian parameters that were found accurately, so this IBFFM model is considered one of the effective models in studying the nuclear structure of odd-odd nuclei. The level density of the odd-odd nucleus 196Au is investigated in the interacting boson-fermion-fermion model (IBFFM) which accounts for collectivity and complex interaction between quasiparticle and collective modes. The IBFFM spin-dependent level densities show high-spin reduction with respect to Bethe formula. This can be well accounted for by a modified spin-dependent level density formula.
},
year = {2024}
}
TY - JOUR T1 - An Application of Interacting Boson Fermion-Fermion Model (IBFFM) for 134Cs Nucleus AU - Afrah Jawad Mohaisen AU - Saad Naji Abood Y1 - 2024/04/17 PY - 2024 N1 - https://doi.org/10.11648/j.ajme.20241001.12 DO - 10.11648/j.ajme.20241001.12 T2 - American Journal of Modern Energy JF - American Journal of Modern Energy JO - American Journal of Modern Energy SP - 11 EP - 17 PB - Science Publishing Group SN - 2575-3797 UR - https://doi.org/10.11648/j.ajme.20241001.12 AB - This work concerns the calculations of interacting boson fermion-fermion model (IBFFM) for the odd-odd nucleus 134Cs. The energy levels (positive and negative parity states), electric transition probability B(E2), magnetic transition probability B(M1), quadrupole and magnetic dipole moments have been studied in this work. The IBFFM results are compared with the available experimental data. In the present work, the IBFFM pattern of total and parametric dependent level densities for the odd-odd nucleus 134Cs is investigated and compared to the pattern found in previous investigations in the framework of combinatorial and spectral distribution approaches. When comparing the theoretical values with the available experimental values, it was found that there is a good match between them. This is due to the values of the Hamiltonian parameters that were found accurately, so this IBFFM model is considered one of the effective models in studying the nuclear structure of odd-odd nuclei. The level density of the odd-odd nucleus 196Au is investigated in the interacting boson-fermion-fermion model (IBFFM) which accounts for collectivity and complex interaction between quasiparticle and collective modes. The IBFFM spin-dependent level densities show high-spin reduction with respect to Bethe formula. This can be well accounted for by a modified spin-dependent level density formula. VL - 10 IS - 1 ER -