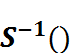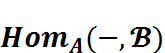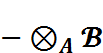Functors <img width="72" height="53" src="http://article.sciencepublishinggroup.com/journal/347/3471098/image001.png" />, <img width="165" height="53" src="http://article.sciencepublishinggroup.com/journal/347/3471098/image002.png" />, <img width="103" height="53" src="http://article.sciencepublishinggroup.com/journal/347/3471098/image003.png" /> and <img width="146" height="53" src="http://article.sciencepublishinggroup.com/journal/347/3471098/image004.png" />in the Category of <i>A - Alg</i>

Moussa Thiaw; Mohamed Ben Faraj Ben Maaouia; Mamadou Sanghare

doi:doi:10.11648/j.ijtam.20190501.11

| Peer-Reviewed

Functors , , and 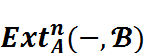in the Category of A - Alg

Moussa Thiaw, Mohamed Ben Faraj Ben Maaouia, Mamadou Sanghare

Published in International Journal of Theoretical and Applied Mathematics (Volume 5, Issue 1)

Received: 18 February 2019 Accepted: 26 March 2019 Published: 18 April 2019

Views: Downloads:

Download PDF

Share This Article

Twitter
Linked In
Facebook

Abstract

The purpose of this paper is to study some results of homological algebra in the category A-Alg (resp. Alg-A) of left (resp. right) A-algebra in the noncommutative case. In this paper A is a subring of B. So the main results of this paper are, if B is a noetherian duo-ring, S a central saturated multiplicatively closed subset of A, S_R the set of regular elements of S, a finitely presented right A-algebra and a (B-A)-bialgebra, then is isomorphic to , also is isomorphic to , for any integer n.

Published in	International Journal of Theoretical and Applied Mathematics (Volume 5, Issue 1)
DOI	10.11648/j.ijtam.20190501.11
Page(s)	1-9
Creative Commons	This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
Copyright	Copyright © The Author(s), 2019. Published by Science Publishing Group

Keywords

Algebra, Multiplicatively Closed Subset, Ore Condition of Multiplicatively Closed Subset, Localized, Category, Functor, Complex Projective Resolution

References

[1]	F. W. Anderson Kent R.Fuller, Rings and Categories of Modules, Springer-Verlag New York, 1974, 1992 Inc.
[2]	M. F. Atiyah and I.G.Macdonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Company, University of Oxford.
[3]	H. Cartan and Samuel Eilenberg, Homological Agebra, Princeton University Press, New Jersey, 1956.
[4]	F. Dennis, Noncommutative algebra, GTM Vol.144, Springer-Verlag, 1993.
[5]	M. P. Eelbert, Localisation in Duo-ring, Kansas.Ciry, Missouri.
[6]	M. F. Maaouia and al, Functor S^-1 () and Adjoint Isomorphism, International Mathematical Forum, vol. 11, 2016, no. 5, 227-237.
[7]	N. Jacobson, Structure of rings, Amer.Math.Soc.Colloquium Publications, Vol.37, 1956.
[8]	D. M. Kan, Adjoint functors, Trans. Amer. Math. Soc. 87 (1958), 294-329.
[9]	Lam, A First Course in Noncommutative Rings, GTM Vol.131, Springer-Verlag, 2001.
[10]	M. F. Maaouia and al., Localization in a Duo-Ring and Polynomials Algebra, Springer International Publishing Switzerland 2016 C.T. Gueye, M.S. Molina (eds.), Non-Associative and Non-Commutative Algebra and Operator Theory, Springer Proceedings in Mathematics and Statistics 160, DOI 10.1007 978-3-319-32902-4-13.
[11]	M. F. Maaouia, Thèse d’état, Faculté des Sciences et Techniques, UCAD, Dakar, Juillet, 2011.
[12]	M. F. Maaouia, Doctorat 3ème Cycle, Faculté des Sciences et Techniques, UCAD, Dakar, Juillet, 2003.
[13]	M. F. Maaouia and M.Sanghare, Localisation Dans Les Duo-Anneaux, Afrika Mathematika, 2009.
[14]	M. F. Maaouia and M.Sanghare, Module de fraction- Sous-modules S-saturée et foncteur S^-1, International Journal of Algebra, 16(2012), 0973-1768.
[15]	M. F. Maaouia and M.Sanghare, Anneau de valuation non nécessairement commutatif et duo-anneau de Dideking, Global Journal of Pure and Applied Mathematics, ISSN 0973-1768 Volume 8, Number 1(2012).
[16]	H. Matsumura, Commutative algebra, W.A. Benjamin, New-York, 1970.
[17]	R. Pierce, Associative Algebras, Grad.Text in Math.88, Springer, 1982.
[18]	J. Rotman, Notes on Homological Algebra, University of Illinois, Urbane, 1968.
[19]	J. Rotman, An introduction to Homological Algebra, GSM Vol.114, Academic Press, New York 1972.

Cite This Article

Plain Text BibTeX RIS

APA Style

Moussa Thiaw, Mohamed Ben Faraj Ben Maaouia, Mamadou Sanghare. (2019). Functors , , and in the Category of A - Alg. International Journal of Theoretical and Applied Mathematics, 5(1), 1-9. https://doi.org/10.11648/j.ijtam.20190501.11

Copy | Download

ACS Style

Moussa Thiaw; Mohamed Ben Faraj Ben Maaouia; Mamadou Sanghare. Functors , , and in the Category of A - Alg. Int. J. Theor. Appl. Math. 2019, 5(1), 1-9. doi: 10.11648/j.ijtam.20190501.11

Copy | Download

AMA Style

Moussa Thiaw, Mohamed Ben Faraj Ben Maaouia, Mamadou Sanghare. Functors , , and in the Category of A - Alg. Int J Theor Appl Math. 2019;5(1):1-9. doi: 10.11648/j.ijtam.20190501.11

Copy | Download

@article{10.11648/j.ijtam.20190501.11,
  author = {Moussa Thiaw and Mohamed Ben Faraj Ben Maaouia and Mamadou Sanghare},
  title = {Functors , ,  and in the Category of A - Alg},
  journal = {International Journal of Theoretical and Applied Mathematics},
  volume = {5},
  number = {1},
  pages = {1-9},
  doi = {10.11648/j.ijtam.20190501.11},
  url = {https://doi.org/10.11648/j.ijtam.20190501.11},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijtam.20190501.11},
  abstract = {The purpose of this paper is to study some results of homological algebra in the category A-Alg (resp. Alg-A) of left (resp. right) A-algebra in the noncommutative case. In this paper A is a subring of B. So the main results of this paper are, if B is a noetherian duo-ring, S a central saturated multiplicatively closed subset of A, SR the set of regular elements of S,  a finitely presented right A-algebra and  a (B-A)-bialgebra, then  is isomorphic to , also  is isomorphic to , for any integer n.},
 year = {2019}
}

Copy | Download

TY  - JOUR
T1  - Functors , ,  and in the Category of A - Alg
AU  - Moussa Thiaw
AU  - Mohamed Ben Faraj Ben Maaouia
AU  - Mamadou Sanghare
Y1  - 2019/04/18
PY  - 2019
N1  - https://doi.org/10.11648/j.ijtam.20190501.11
DO  - 10.11648/j.ijtam.20190501.11
T2  - International Journal of Theoretical and Applied Mathematics
JF  - International Journal of Theoretical and Applied Mathematics
JO  - International Journal of Theoretical and Applied Mathematics
SP  - 1
EP  - 9
PB  - Science Publishing Group
SN  - 2575-5080
UR  - https://doi.org/10.11648/j.ijtam.20190501.11
AB  - The purpose of this paper is to study some results of homological algebra in the category A-Alg (resp. Alg-A) of left (resp. right) A-algebra in the noncommutative case. In this paper A is a subring of B. So the main results of this paper are, if B is a noetherian duo-ring, S a central saturated multiplicatively closed subset of A, SR the set of regular elements of S,  a finitely presented right A-algebra and  a (B-A)-bialgebra, then  is isomorphic to , also  is isomorphic to , for any integer n.
VL  - 5
IS  - 1
ER  -

Copy | Download

Author Information

Moussa Thiaw

UFR of Applied Sciences and Technology, Gaston Berger University, Saint-Louis, Senegal
Mohamed Ben Faraj Ben Maaouia

UFR of Applied Sciences and Technology, Gaston Berger University, Saint-Louis, Senegal
Mamadou Sanghare

Department of Mathematics, Faculty of Science and Technology, Cheikh Anta Diop University, Dakar, Senegal

Download PDF

Sections

Plain Text BibTeX RIS

APA Style

Moussa Thiaw, Mohamed Ben Faraj Ben Maaouia, Mamadou Sanghare. (2019). Functors , , and in the Category of A - Alg. International Journal of Theoretical and Applied Mathematics, 5(1), 1-9. https://doi.org/10.11648/j.ijtam.20190501.11

Copy | Download

ACS Style

Moussa Thiaw; Mohamed Ben Faraj Ben Maaouia; Mamadou Sanghare. Functors , , and in the Category of A - Alg. Int. J. Theor. Appl. Math. 2019, 5(1), 1-9. doi: 10.11648/j.ijtam.20190501.11

Copy | Download

AMA Style

Moussa Thiaw, Mohamed Ben Faraj Ben Maaouia, Mamadou Sanghare. Functors , , and in the Category of A - Alg. Int J Theor Appl Math. 2019;5(1):1-9. doi: 10.11648/j.ijtam.20190501.11

Copy | Download

@article{10.11648/j.ijtam.20190501.11,
  author = {Moussa Thiaw and Mohamed Ben Faraj Ben Maaouia and Mamadou Sanghare},
  title = {Functors , ,  and in the Category of A - Alg},
  journal = {International Journal of Theoretical and Applied Mathematics},
  volume = {5},
  number = {1},
  pages = {1-9},
  doi = {10.11648/j.ijtam.20190501.11},
  url = {https://doi.org/10.11648/j.ijtam.20190501.11},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijtam.20190501.11},
  abstract = {The purpose of this paper is to study some results of homological algebra in the category A-Alg (resp. Alg-A) of left (resp. right) A-algebra in the noncommutative case. In this paper A is a subring of B. So the main results of this paper are, if B is a noetherian duo-ring, S a central saturated multiplicatively closed subset of A, SR the set of regular elements of S,  a finitely presented right A-algebra and  a (B-A)-bialgebra, then  is isomorphic to , also  is isomorphic to , for any integer n.},
 year = {2019}
}

Copy | Download

TY  - JOUR
T1  - Functors , ,  and in the Category of A - Alg
AU  - Moussa Thiaw
AU  - Mohamed Ben Faraj Ben Maaouia
AU  - Mamadou Sanghare
Y1  - 2019/04/18
PY  - 2019
N1  - https://doi.org/10.11648/j.ijtam.20190501.11
DO  - 10.11648/j.ijtam.20190501.11
T2  - International Journal of Theoretical and Applied Mathematics
JF  - International Journal of Theoretical and Applied Mathematics
JO  - International Journal of Theoretical and Applied Mathematics
SP  - 1
EP  - 9
PB  - Science Publishing Group
SN  - 2575-5080
UR  - https://doi.org/10.11648/j.ijtam.20190501.11
AB  - The purpose of this paper is to study some results of homological algebra in the category A-Alg (resp. Alg-A) of left (resp. right) A-algebra in the noncommutative case. In this paper A is a subring of B. So the main results of this paper are, if B is a noetherian duo-ring, S a central saturated multiplicatively closed subset of A, SR the set of regular elements of S,  a finitely presented right A-algebra and  a (B-A)-bialgebra, then  is isomorphic to , also  is isomorphic to , for any integer n.
VL  - 5
IS  - 1
ER  -

Copy | Download