Abstract
The numerical integration of Hamiltonian systems with oscillating solutions is considered in this paper. Since Hamiltonian systems have good properties such as symplecticity, numerical methods that preserve these properties have attracted the great attention. In fact, the explicit Runge-Kutta methods have used due to that schemes are very simple and its computational amounts are very small. However, the explicit schemes aren’t stable so the implicit Runge-Kutta methods have widely studied. Among those implicit schemes, symplectic numerical methods were interested. It is because it has preserved the original property of the systems. So, study of the symplectic Runge-Kutta methods have performed. The typical symplectic Runge-Kutta method is the Gauss-Legendre method, whose drawback is that it is a general implicit scheme and is too computationally expensive. Despite these drawbacks, the study of the diagonally implicit symplectic Runge-Kutta methods that preserves symplecticity has attracted much attention. The symplectic Runge-Kutta method has been studied up to sixth order in the past and efforts to obtain higher order conditions and algorithms are being intensified. In many applications such as molecular dynamics as well as in space science, such as satellite relative motion studies, this method is very effective and its application is wider. In this paper, it is presented the 7th order condition and derive the corresponding optimized method. So the diagonally implicit symplectic eleven-stages Runge-Kutta method with algebraic order 7 and dispersion order 8 is presented. Numerical experiments with some Hamiltonian oscillatory problems are presented to show the proposed method is as competitive as the existing same type Runge-Kutta methods.
Keywords
Diagonally Implicit Scheme, Seventh Order, Symplectic Runge-Kutta Method
1. Introduction
In the past decades, there have been numerous researches performed in the area of the numerical symplectic integration of Hamiltonian systems
| [29] | Z. Kalogiratou, Th. Monovasilis. Diagonally Implicit Symplectic Runge-Kutta Methods with Special Properties, Appli. Mathe. & Infor. Scie, Feb. 2015, http://dx.doi.org/10.12785/amis/091L02 |
[29]
, Hamiltonian system of differential equations can be expressed as:
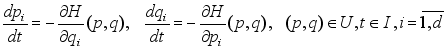 (1)
(1) where is a twice continuously differentiable function and is an open set.
For example, Mathematical Pendulum, Newton’s motion equation, Equation for molecular dynamics and High frequency equation can be considered as Hamiltonian systems
| [5] | E. Hairer, C. Lubich, G. Wanner. Geometric Numerical Integration. Structure Preserving Algorithms for Ordinary Differential Equations, 2nd ed, Springer, Berlin, 2006. https://doi.org/10.1007/3-540-30666- 8 |
| [24] | V. I. Amold. Mathematical Methods of Classical Mechanics, Springer-Berlin, 1999. |
[5, 24]
.
Hamiltonian systems often arise in different fields of applied sciences such as celestial mechanics, astrophysics, chemistry, electronics, and molecular dynamics
| [7] | G. Avdelas, A. Konguetsof, T. E. Simos. A generator and an optimized generator of high-order hybrid explicit methods for the numerical solution of the Schrodinger equation. Part 1. Deveolpment of the basic method, J. Math. Chem, 2001, 29, 281291. https://doi.org/10.1016/S0010-4655(02)00468-X |
| [18] | K. Tselios, T. E. Simos. Runge-Kutta methods with minimal dispersion and dissipation for problems arising from computational acoustics, Journal of Computational and Applied Mathematics, 2005, 175(1), 173-181. https://doi.org/10.1142/9789812704658_0142 |
| [22] | Run-de Zhang, Le-ping Yang, Wei-wei Cai. Symplectic Runge-Kutta Method Based Numerical Solution for the Hamiltonian Model of Spacecraft Relative Motion, Springer Nature Singapore Pte Ltd, 2019, https://doi.org/10.1007/978-981-13-3305-7_171 |
[7, 18, 22]
.
The range of Nano physical developments with Hamiltonian models contains wide ranges from molecular dynamics to celestial mechanics
| [14] | J. M. Sanz-Serna, M. P. Calvo. Numerical Hamiltonian Problems, Champman and Hall, London, 1994. |
| [15] | Kaifeng Xia, Yuhao Cong, Geng Sun. Symplectic Runge-Kutta Methods of high order based on W-transformation, Journal of Applied Analysis and Computation, 2017, 7(3), https://doi.org/10.11948/2017074 |
| [23] | U. Ascher, S. Reich. On some difficulties in integrating highly oscillatory Hamiltonian systems, in Computational Molecular Dynamics, Lecture Notes in Comput. Sci. Engrg. 4, Springer, Berlin, 1999, 281-296. |
[14, 15, 23]
.
The feature of Hamiltonian system is that this system satisfies classical conservation laws such as law of conservation of energy and also satisfies law of conservation of symplectic property.
Generally, the differential equations that are expressed as mathematical modeling of these problems are solved numerically using the numerical methods. But the numerical solutions of differential equations are contained a little error.
The most important problem in developing numerical methods is to construct the schemes with minimized error. But some schemes don’t reflect the main symplectic property. So in the 1980s the opinion that the numerical methods for solving the mathematical models have to preserve the system’s main property was presented
| [5] | E. Hairer, C. Lubich, G. Wanner. Geometric Numerical Integration. Structure Preserving Algorithms for Ordinary Differential Equations, 2nd ed, Springer, Berlin, 2006. https://doi.org/10.1007/3-540-30666- 8 |
| [17] | K. Feng. Collected Works of Feng Kang (II), National Defence Press, Beijing, 1995. |
[5, 17]
.
The advantages of such methods are well demonstrated in problems that are difficult to solve by classical methods, for example, problems with singularities, problems with long-term calculations, and the analysis of highly oscillatory systems.
Since the symplectic is a property of Hamiltonian systems, numerical methods with this property have been studied.
Such a previous work can be found in Hairer, Lubich, Wanner, Sanz Serna, and Calvo.
.
The earliest work on symplectic numerical methods can be found in Vogelaere’s the paper in 1956 and Ruth’s paper in 1983
| [3] | E. Hairer, G. Wanner. Symplectic Runge-Kutta methods with real eigenvalues. BIT Nume, Mathe, 1994, 34(2), 310-312. |
| [28] | Y. L. Fang, Q. H. Li. A class of explicit rational symplectic integrators, Journal of Applied Analysis and Computation, 2012, 2(2), 161-171. https://doi.org/10.11948/2012012 |
[3, 28]
.
Ruth constructed partitioned symplectic Runge-Kutta method with third order.
Since about 1988, the symplectic order condition has been independently derived by Suris, Lasagni, and Sanz-Serna, respectively, and the symplectic Runge-Kutta method has been studied extensively
| [1] | A. Iserles. Efficient Runge-Kutta methods for Hamiltonian equations. Bulletin of the Greek Mathematical Society, 1991, 32, 3-20, https://doi.org/10.1142/9789814354561_0008 |
| [4] | E. Hairer, C. Lubich, G. Wanner. Geometric Numerical Integration: Structure Preserving Algorithms for Ordinary Differential Equations, Springer, Berlin, Germany, 1994, 2002. |
| [30] | Z. Kalogiratou, T. Monovasilis, T. E. Simos. A diagonally implicit symplectic Runge-Kutta method with minimum phase-lag, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 11), vol. 1389 of AIP Conference Proceedings, 2011, 1977-1979, https://doi.org/10.1063/1.3637001 |
[1, 4, 30]
.
Since the solution of the system of ordinary differential equations (
1) exhibits oscillatory character in almost cases, the numerical solution of the oscillating Hamiltonian system must be constructed by considering both symplecticity and oscillatory character simultaneously.
The phase-lag analysis, which reflects the oscillation property, was introduced by Brusa and Nigro
| [19] | L. Brusa, L. Nigro. A one-step method for direct integration of structural dynamic equations, International Journal for Numerical Methods in Engineering, 1980, 15(5), 685-699. https://doi.org/10.1002/nme.1620150506 |
[19]
.
The phase-lag analysis is evaluated in terms of the dispersion order.
In the past few years, there has been an increasing interest in constructing symplectic Runge-Kutta methods for the oscillatory problems
| [1] | A. Iserles. Efficient Runge-Kutta methods for Hamiltonian equations. Bulletin of the Greek Mathematical Society, 1991, 32, 3-20, https://doi.org/10.1142/9789814354561_0008 |
| [10] | H. van de Vyer. Fourth order symplectic integration with reduced phase error, International Journal of Modern Physics C, 2008, 19(8), 1257-1268. |
| [30] | Z. Kalogiratou, T. Monovasilis, T. E. Simos. A diagonally implicit symplectic Runge-Kutta method with minimum phase-lag, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 11), vol. 1389 of AIP Conference Proceedings, 2011, 1977-1979, https://doi.org/10.1063/1.3637001 |
| [31] | Z. Kalogiratou, T. Monovasilis, T. E. Simos. Diagonally implicit symplectic Runge-Kutta method with special properties, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 12), 1479 of AIP Conference Proceedings, 2012, 1387-1390, https://doi.org/10.1063/1.4756416 |
[1, 10, 30, 31]
.
In Hairer and Wanner, it is constructed the symplectic Runge-Kutta method using the W-transformation
| [3] | E. Hairer, G. Wanner. Symplectic Runge-Kutta methods with real eigenvalues. BIT Nume, Mathe, 1994, 34(2), 310-312. |
[3]
.
In Iserles, it is constructed the symplectic Runge-Kutta method with real eigenvalues with the help of perturbation configuration
.
In Sun, it is given a simple method to obtain the symplectic method with the help of the symplecticity condition of the partitioned Runge-Kutta method
| [8] | Geng Sun. A simple way constructing symplectic Runge-Kutta methods. J. Comput. Mathe, 2000, 18(1), 61-68. |
[8]
.
Recently, the attention has been paid to the diagonally implicit symplectic Runge-Kutta method, which has been studied by Suris, Qin, Zhang, Kalogiratou et al, Cong, Jiang, Franco, and Gomez
| [10] | H. van de Vyer. Fourth order symplectic integration with reduced phase error, International Journal of Modern Physics C, 2008, 19(8), 1257-1268. |
| [13] | J. M. Franco, I. Gomez. Fourth-order symmetric DIRK methods for periodic stiff problems, Numerical Algorithms, 2003, 32(24), 317-326. https://doi.org/10.1023/A:1024077930017 |
| [20] | M. Z. Qin, M. Q. Zhang. Symplectic Runge-Kutta algorithmz for Hamilton systems, Journal of Computational Mathematics, Supplementary Issue, 1992, 205-215. |
| [25] | Y. B. Suris. Canonical transformation generated by methods of Runge-Kutta type for the numerical integration of the system x´´=-∂U/∂x, Zhurnal Vychisliteli Matermatiki I Mathematics, 2005, 175(1), 173-181. |
| [26] | Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods of fifth and sixth order, The Scientific World Journal, 2014, https://doi.org/10.1155/2014/147801 |
| [30] | Z. Kalogiratou, T. Monovasilis, T. E. Simos. A diagonally implicit symplectic Runge-Kutta method with minimum phase-lag, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 11), vol. 1389 of AIP Conference Proceedings, 2011, 1977-1979, https://doi.org/10.1063/1.3637001 |
| [31] | Z. Kalogiratou, T. Monovasilis, T. E. Simos. Diagonally implicit symplectic Runge-Kutta method with special properties, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 12), 1479 of AIP Conference Proceedings, 2012, 1387-1390, https://doi.org/10.1063/1.4756416 |
[10, 13, 20, 25, 26, 30, 31]
.
In Franco and Gomez, it is constructed symplectic diagonally implicit Runge-Kutta method of algebraic order 4 and phase-lag order 6 with five stages
.
In Z. Kalogiratou et al. it is constructed symplectic diagonally implicit Runge-Kutta method of algebraic order 5 and phase-lag order 6 with seven stages
| [31] | Z. Kalogiratou, T. Monovasilis, T. E. Simos. Diagonally implicit symplectic Runge-Kutta method with special properties, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 12), 1479 of AIP Conference Proceedings, 2012, 1387-1390, https://doi.org/10.1063/1.4756416 |
[31]
.
It is interesting to note here that the order condition for the fifth algebraic order is constructed.
In Cong and Jiang, it is constructed the symplectic diagonally implicit Runge-Kutta method of algebraic order 6 and phase-lag order 8 with nine stages
| [9] | Geng Sun. Symmetric-Adjoint and Symplectic-Adjoint Runge-Kutta Methods and Their Applications, Numer. Math. Theor. Meth. Appl, 2022, 15(2), 304-335, https://doi.org/10.4208/nmtma.OA-2021-0097 |
| [11] | J. C. Butcher. A history of Runge-Kutta methods, Applied Numerical Mathematics, 1996, 20, 257-260. |
| [27] | Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods with High Algebraic and Dispersion Order, The Scientific World Journal, 2014, Article ID 147801, 7, http://dx.doi.org/10.1155/2014/147801 |
[9, 11, 27]
.
It is interesting to note here that the order condition of the sixth algebraic order is constructed.
The important problem in actually constructing the schemes is to find the exactly order condition that the scheme must satisfy.
However, in general, it is difficult to visualize Taylor expansions of differential equations, and this work carried out in the fields such as W-transform techniques, rooted tree theory and so on
| [2] | Ch. Tsitouras. Explicit Runge-Kutta methods for starting integration of Lane-Emden problem. Appl. Mathe. Comput, 2019, 354, 353-364, https://doi.org/10.1016/j.amc.2019.02.047 |
| [15] | Kaifeng Xia, Yuhao Cong, Geng Sun. Symplectic Runge-Kutta Methods of high order based on W-transformation, Journal of Applied Analysis and Computation, 2017, 7(3), https://doi.org/10.11948/2017074 |
[2, 15]
.
An attempt to derive the convergence order condition using the rooted tree theory was made in the case of the general Runge-Kutta method but it was not found how to construct a rooted tree satisfying symplectic property.
To summarize the previous results, numerical methods for the Hamiltonian systems with oscillatory character have been studied in the direction of increasing their algebraic and dispersion orders.
However, the computational speed cannot be guaranteed or even is almost impossible due to the increased computational effort at the same time as the order increases, and the study of the diagonally implicit symplectic Runge-Kutta method with special properties is being intensified.
This is very useful in solving practical problems, for it is computationally very small compared with the conventional implicit scheme and provides the stability.
Therefore, It is given firstly some basic knowledges about the dispersion properties of the Runge-Kutta method, the symplecticity conditions of the Runge-Kutta method, the properties of the diagonally implicit symplectic Runge-Kutta method, the root tree theory and so on.
Next, It is derived the diagonally implicit symplectic Runge-Kutta schemes with the seventh order condition and study the stability and dispersion properties of the proposed method based on it.
In addition, numerical experiments investigating the Hamiltonians by the proposed Runge-Kutta method are carried out to confirm its superiority.
2. Preliminary Knowledge
2.1. The Computational Schemes of the Runge-Kutta Method
Consider the following initial value problem for ordinary differential equation.
(2)
In general, the schemes of the s-stages Runge-Kutta method is defined as follows
| [27] | Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods with High Algebraic and Dispersion Order, The Scientific World Journal, 2014, Article ID 147801, 7, http://dx.doi.org/10.1155/2014/147801 |
[27]
.
(3)
where are real parameters.
This scheme is called the Butcher tableau
.
If , then the all can be computed in an explicit way from . Therefore such scheme is called explicit Runge-Kutta scheme.
In scheme (
3), when
, and has certain
in diagonal line
, the scheme is called diagonally implicit scheme.
If the method is neither explicit, nor diagonally implicit, it is just called implicit
.
2.2. Symplecticity Condition of Runge-Kutta Method
Make the following symbolic convention.
Theorem 1.
| [29] | Z. Kalogiratou, Th. Monovasilis. Diagonally Implicit Symplectic Runge-Kutta Methods with Special Properties, Appli. Mathe. & Infor. Scie, Feb. 2015, http://dx.doi.org/10.12785/amis/091L02 |
[29]
If(4)
Then, the s-stages Runge-Kutta method is symplectic.
2.3. Order Condition of Runge-Kutta Method
Applying the Runge-Kutta method to equation (
2), the corresponding Taylor expansion can be found
| [6] | E. Hairer, S. P. Norsett, G. Wanner, Solving Ordinary Differential Equations I, second ed., Springer, Heidelberg, 1993. |
[6]
.
(5)
All derivatives are found at the point .
Simultaneously It is expanded of Runge-Kutta method around the point .
For example,
(6)
Thus,
(7)
Here are determined by the coefficients .
Subtract (
7) from (
5), and then get the local truncation error.
(8)
When the local truncation error of RK method is , then the RK method has order p. Then in the expression above the coefficients are zero for powers of h up to p. Thus, for a RK method to attain order p that have to satisfy various equations called order conditions.
2.4. Rooted Tree Theory
The basic method to construct the numerical scheme for ordinary differential equation is Taylor expansion. If only a single (scalar) equation is considered, Taylor expansion can be used in studying the convergence, compatibility, and order conditions for RK methods. However, if the system of differential equations are considered, Taylor expansion is intractable.
The second order derivative can be expressed by the Jacobian matrix.
However, the third-order derivative can no longer be expressed by via matrix and vector symbol, not to mention the higher order derivative. This has motivated people to study the structure of the Taylor expansion of high order derivatives and search for a better symbol to simplify the Taylor expansion of high order derivatives. Then the rooted tree theory emerged.
Definition 1.
| [12] | J. C. Simo, N. Tarnow. A new energy and momentum conserving algorithm for the nonlinear dynamics of shells, Internet. J. Numer. Methods Engrg., 1994, 37, 2527-2549. https://doi.org/10.1002/nme.1620371503 |
[12]
The directed graphs containing a root is called a rooted tree.
If you choose different roots, the rooted tree will also be different.
Let T denote the set of rooted trees.
The rooted tree with up to four vertices is given in the
Figure 1.
Figure 1. The rooted tree with up to fourth order.
Here the root is conveniently made to be the lowest vertex.
Rooted tree theory is a theory that introduces the concept of a rooted tree used in graph theory to denote higher-order derivatives to determine the order condition.
2.5. Phase-Lag Analysis
The application of a Runge-Kutta method to the test problem
leads to the numerical scheme.
(11)
(12)
Where depend only on the coefficients of the methods.
Definition 2.
| [12] | J. C. Simo, N. Tarnow. A new energy and momentum conserving algorithm for the nonlinear dynamics of shells, Internet. J. Numer. Methods Engrg., 1994, 37, 2527-2549. https://doi.org/10.1002/nme.1620371503 |
[12]
For a Runge-Kutta method the dispersion error (Phase-lag error) is given by
If , then the Runge-Kutta method is said to have dispersion order q.
Moreover, if consider the stability function and collect the real and imaginary parts
then the dispersion errors can be written in the form
An alternative form for is
(16)
For symplectic Runge-Kutta methods always have
(17)
Lemma 1.
| [21] | P. J. van der Houwen, B. P. Sommejier. Phase-lag analysis of implicit Runge-Kutta methods, SIAM J. Numer. Anal, 1989, 26(1), 214-229, https://doi.org/10.1137/0726012 |
[21]
A RK method is dispersive of order
q, if the coefficients
in the
satisfy the following conditions:
(18)
3. Construction of the New Method
Compared with the conventional RK methods and the SRK method has a very small number of conditions for determining the order for the accuracy, because the symplectic condition plays the same role as the simplification assumption.
A comparison of the number of conditions that determine the convergence order of the conventional
RK method and the
SRK method is shown in the
Table 1.
Now, to determine the order condition of the SRK method, let us construct the rooted tree by introducing the rooted tree theory.
Definition 3. The order , symmetry , and density (tree factorial) are defined by
(20)
(21)
(22)
Table 1. Order conditions of RK and SRK.
Order | RK | SRK |
1 | 1 | 1 |
2 | 2 | 1 |
3 | 4 | 3 |
4 | 8 | 4 |
5 | 17 | 6 |
6 | 37 | 10 |
7 | 85 | 21 |
Higher order rooted trees can be constructed by grafting new vertices onto the rooted tree with one vertex .
Let (tree multiplicity) be the number of essentially different ways of labeling the vertices of the tree with integers such that labels are monotonously increases.
can expressed by (
23), namely,
Define the following functions to map a set of trees to a set of functions.
Definition 4.
1) For , define the function of , on the set T of all trees by:
(25)
2) Define
Theorem 2
| [16] | Kang Feng, Mengzhao Qin. Symplectic Geometric Algorithms for Hamiltonian Systems, Zhejiang Publishing United Group, Zhejiang Science and Technology Publishing House, 2009, 277-302. https://doi.org/10.1007/978-3-642-01777-3 |
[16]
.
RK method has order p, if
(27)
And does not hold for some trees of order .
From the Theorem 2, it can judge the convergence with the tree if it is constructed.
There are four types of trees, which can be defined as follows
| [16] | Kang Feng, Mengzhao Qin. Symplectic Geometric Algorithms for Hamiltonian Systems, Zhejiang Publishing United Group, Zhejiang Science and Technology Publishing House, 2009, 277-302. https://doi.org/10.1007/978-3-642-01777-3 |
[16]
:
(1) A labeled tree is a labeled graph {V, E}, such that for any pair of distinct vertices and , there exists a unique path that joins and .
(2) Two labeled trees and are said to be isomorphic, if a bijection of onto exists that transforms edges in into edges in , vertices into . The trees is an equivalence class that consists of labeled trees isomorphic to it. Each of the labeled tree that represent is called a labeling of .
(3) A rooted labeled tree is a labeled tree, in which one of the vertices , called the root, has been highlighted. The vertices adjacent to the root are called the sons of the root. The sons of the remaining vertices are defined in the relationship between father and son. Let be a mapping from son to father. Since any point has a path to the root, e.g. may be obtained through the sequential action of on .
Therefore a direction can be defined from to , and the entire root also become oriented.
(4) Two labeled trees , are said to be root isomorphic, if a bijection of onto exists that transforms edges in onto and maps onto . A rooted trees is an equivalence class that comprises of the rooted labeled tree and all rooted labeled trees root-isomorphic to it.
Definition 5. Let be an n-tree and choose one of its labeling . This labeling gives rise to different rooted labeled trees , where has its root at the integer . If for each edge in , and represent different rooted trees; then is called non-superfluous.
Example 1. Labeled 3-tree is non-superfluous and labeled 4-tree is superfluous.
Consider the 3-tree .
When choosing the labeled 3-tree, can see that for the edge 1-2, choosing 1 as the root leads to , choosing 2 as the root leads to . For the edge 2-3, choosing 2 as the root leads to , and choosing 3 as the root leads to .
Therefore is non-superfluous.
On the other hand the 4-tree with labeling is superfluous, since changing the root from 2 to the adjacent 3 does not result in different rooted trees.
Figure 2. Rooted trees in Lemma.
Look at first rooted tree
and
. The root of the rooted trees
,
in
Figure 2 is at vertex
i and
j, they are removed edge joining I and J in the top left-hand corner graph.
Lemma 2. With the above notations
1)
(28)
2) For the symplectic RK method, weighted coefficients of elementary differential satisfy
3) For order , symplectic RK method,
(30)
Therefore order conditions holds if order conditions of hold.
Proof.
1) By the definition of ,
(31)
(32)
In the formula,
(33)
Thus,
2)
(34)
Where represents a product of factors .
Using the order condition of the SRK method (4).
(35)
Thus,
3) From 2),
(36)
Theorem 3. Assume that a symplectic RK method satisfies the order conditions for order with . Then, to ensure that the method have order , it is sufficient that, for each non-superfluous tree with r vertices, there is at least one rooted tree associated with for which
Proof. Choose the first a non-superfluous tree .
Assume that the condition (
27) is satisfied for a suitable rooted tree
of
. From the Lemma 2 choose
as any of the vertices adjacent to
. By the condition (
26), the order condition (
27) is also satisfied for
.
Since any two vertices of a tree can be joined through a chain of pairwise adjacent vertices, the iteration of this argument leads to the conclusion that the method satisfies the order conditions that arise from any rooted tree in
. In the case of a superfluous tree
, by definition, it is possible to choose adjacent vertices
,
, such that
and
are in fact the same rooted tree. Then condition (
26) shows that (
27) holds for the rooted tree
.
Therefore (
27) holds for all rooted tree in
.
For symplectic RK methods it is sufficient to obtain the order conditions only for non-superfluous trees rather than every rooted trees.
Thus, constructing the rooted trees of symplectic Runge-Kutta method up to the seventh orders is shown in the following
Figure 3.
Figure 3. The trees of SRK.
Deriving the convergence order condition for the above the trees of symplectic Runge-Kutta method by Theorem 3, can obtain the
Table 2.
Order conditions of (3) for the 11-stages diagonally implicit SRK method with 7-th order convergence are following as.
Table 2. Rooted trees and order conditions.
T | | | | | Order condition |
| 1 | 1 | 1 | 1 | |
| 3 | 2 | 3 | 1 | |
| 4 | 6 | 4 | 1 | |
| 5 | 24 | 5 | 1 | |
| 5 | 2 | 10 | 6 | |
| 5 | 1 | 20 | 6 | |
| 6 | 120 | 6 | 1 | |
| 6 | 6 | 12 | 10 | |
| 6 | 2 | 24 | 15 | |
| 6 | 2 | 36 | 1 | |
| 7 | 2 | 252 | 10 | |
| 7 | 1 | 84 | 60 | |
| 7 | 6 | 42 | 20 | |
| 7 | 8 | 63 | 10 | |
| 7 | 24 | 14 | 15 | |
| 7 | 4 | 28 | 45 | |
| 7 | 6 | 56 | 15 | |
| 7 | 2 | 42 | 60 | |
| 7 | 720 | 7 | 1 | |
| 7 | 2 | 168 | 15 | |
| 7 | 12 | 21 | 20 | |
To construct an eleven-stage diagonally implicit symplectic Runge-Kutta method with algebraic order 7 and dispersion order 8, it only need to choose the free parameters to minimize the error norm,
Minimizing the error norm, it can get
DISRK method’s parameters in
Table 3.
Table 3. Parameters for the DISRK11,7,8.
Parameter | Value | Parameter | Value |
| 0.0884823 | | 0.0442412 |
| 0.0898123 | | 0.1333885 |
| 0.0931355 | | 0.2248624 |
| 0.0996577 | | 0.321259 |
| 0.112612 | | 0.4273938 |
| 0.145116 | | 0.5562578 |
| 0.246823 | | 0.7522273 |
| -0.333089 | | 0.7090943 |
| 0.24727 | | 0.6661848 |
| 0.122669 | | 0.8511543 |
| 0.0875886 | | 0.9562831 |
4. Stability and Dispersive Error Analysis
4.1. Stability
Considering a scalar test ordinary differential equation,
Applying (
3) to the test equation yields the stability difference equation of the form
(41)
Where R(z) is the stability function of the method and I is an Identity matrix of size , so as if and only if , and the method is absolutely stable for those values of z for which holds.
Definition 6
| [27] | Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods with High Algebraic and Dispersion Order, The Scientific World Journal, 2014, Article ID 147801, 7, http://dx.doi.org/10.1155/2014/147801 |
[27]
. The stability region is defined as
Definition 7
| [27] | Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods with High Algebraic and Dispersion Order, The Scientific World Journal, 2014, Article ID 147801, 7, http://dx.doi.org/10.1155/2014/147801 |
[27]
. A Runge-Kutta method is said to be
A-stable if its stability region contains
, that is, the non-positive half-plane
.
For symplectic Runge-Kutta methods, it always have .
So the new method is A-stable.
The stability region of the new method is illustrated in
Figure 3; from the figure, it can see that the points in the non-positive half-plane and only few points in the right-plane satisfy
; that is, to say the new method
DISRK 11,7,8 it discussed is
A-stable method.
Figure 4. Stability region of the DISRK 11,7,8.
4.2. Dispersion Error
Compare the new method with some already known methods; the methods chosen to be tested are as follows.
M756; diagonally implicit symplectic Runge-Kutta methods with special properties of Kalogiratou et al. are a seven-stage method with algebraic order 5 and dispersion order 6.
M968; diagonally implicit symplectic Runge-Kutta methods with special properties of Y. H. Cong and C. X. Jiang. are a nine-stage method with algebraic order 7 and dispersion order 8.
M11,7,8; is proposed in the paper.
Figure 5 shows the dispersion error of the 3 compared methods.
From the figures, the dispersive error curve of M968 and M11,7,8 appears to overlap, for they have the same dispersive order. On the other hand, the dispersion orders of the M968 and M11,7,8 are the highest ones among the compared 3 methods; the lowest one is the method M756 of Kalogiratou et al.
Figure 5. Difference in dispersion.
In the Figure, Methods used: M11,7,8 is in black. M756 is in red. M968 is in purple.
5. Numerical Experiments
In this numerical study, it is interested in the errors of the Hamiltonian quantity.
1) Harmonic Oscillatory System.
Consider
The Hamiltonian function is
The exact solution is
(45)
where
The problem has been solved numerically in the interval
with several steps. In
table 4 it present the maximum absolute error of the solution.
The error of Hamiltonian for all methods is less than .
Table 4. Maximum absolute error of the solution of the Harmonic Oscillator.
h | M968 | M11,7,8 |
0.2 | | |
0.1 | | |
2) Standard Pendulum.
The Hamiltonian of this problem is given by
The equation of motion are
Consider the problem with initial conditions
The problem has been solved numerically in the interval
with several steps. In
table 5 it present the maximum absolute error of the solution.
Table 5. Maximum absolute error of the solution of the Standard Pendulum.
h | M968 | M11,7,8 |
0.2 | | |
0.1 | | |
0.01 | | |
6. Conclusions
Here it is constructed a 11-stages diagonally implicit symplectic Runge-Kutta method with algebraic order 7 and dispersion order 8. As it can see from the stability region and difference in dispersion, the new method is A-stable method and more easily implemented than general fully implicit methods. The numerical experiments carried out with some oscillatory Hamiltonian systems show that the new method is as competitive as the existing Runge-Kutta methods of the same type.
Abbreviations
RK | Runge-Kutta Method |
SRK | Symplectic Runge-Kutta Method |
DISRK | Diagonally Implicit Symplectic Runge-Kutta Method |
Author Contributions
Thae Gun Oh: Conceptualization, Methodology, Writing – original draft
Ji Hyang Choe: Data curation, Investigation
Jin Sim Kim: Formal Analysis, Investigation, Writing – review & editing
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] |
A. Iserles. Efficient Runge-Kutta methods for Hamiltonian equations. Bulletin of the Greek Mathematical Society, 1991, 32, 3-20,
https://doi.org/10.1142/9789814354561_0008
|
| [2] |
Ch. Tsitouras. Explicit Runge-Kutta methods for starting integration of Lane-Emden problem. Appl. Mathe. Comput, 2019, 354, 353-364,
https://doi.org/10.1016/j.amc.2019.02.047
|
| [3] |
E. Hairer, G. Wanner. Symplectic Runge-Kutta methods with real eigenvalues. BIT Nume, Mathe, 1994, 34(2), 310-312.
|
| [4] |
E. Hairer, C. Lubich, G. Wanner. Geometric Numerical Integration: Structure Preserving Algorithms for Ordinary Differential Equations, Springer, Berlin, Germany, 1994, 2002.
|
| [5] |
E. Hairer, C. Lubich, G. Wanner. Geometric Numerical Integration. Structure Preserving Algorithms for Ordinary Differential Equations, 2nd ed, Springer, Berlin, 2006.
https://doi.org/10.1007/3-540-30666-
8
|
| [6] |
E. Hairer, S. P. Norsett, G. Wanner, Solving Ordinary Differential Equations I, second ed., Springer, Heidelberg, 1993.
|
| [7] |
G. Avdelas, A. Konguetsof, T. E. Simos. A generator and an optimized generator of high-order hybrid explicit methods for the numerical solution of the Schrodinger equation. Part 1. Deveolpment of the basic method, J. Math. Chem, 2001, 29, 281291.
https://doi.org/10.1016/S0010-4655(02)00468-X
|
| [8] |
Geng Sun. A simple way constructing symplectic Runge-Kutta methods. J. Comput. Mathe, 2000, 18(1), 61-68.
|
| [9] |
Geng Sun. Symmetric-Adjoint and Symplectic-Adjoint Runge-Kutta Methods and Their Applications, Numer. Math. Theor. Meth. Appl, 2022, 15(2), 304-335,
https://doi.org/10.4208/nmtma.OA-2021-0097
|
| [10] |
H. van de Vyer. Fourth order symplectic integration with reduced phase error, International Journal of Modern Physics C, 2008, 19(8), 1257-1268.
|
| [11] |
J. C. Butcher. A history of Runge-Kutta methods, Applied Numerical Mathematics, 1996, 20, 257-260.
|
| [12] |
J. C. Simo, N. Tarnow. A new energy and momentum conserving algorithm for the nonlinear dynamics of shells, Internet. J. Numer. Methods Engrg., 1994, 37, 2527-2549.
https://doi.org/10.1002/nme.1620371503
|
| [13] |
J. M. Franco, I. Gomez. Fourth-order symmetric DIRK methods for periodic stiff problems, Numerical Algorithms, 2003, 32(24), 317-326.
https://doi.org/10.1023/A:1024077930017
|
| [14] |
J. M. Sanz-Serna, M. P. Calvo. Numerical Hamiltonian Problems, Champman and Hall, London, 1994.
|
| [15] |
Kaifeng Xia, Yuhao Cong, Geng Sun. Symplectic Runge-Kutta Methods of high order based on W-transformation, Journal of Applied Analysis and Computation, 2017, 7(3),
https://doi.org/10.11948/2017074
|
| [16] |
Kang Feng, Mengzhao Qin. Symplectic Geometric Algorithms for Hamiltonian Systems, Zhejiang Publishing United Group, Zhejiang Science and Technology Publishing House, 2009, 277-302.
https://doi.org/10.1007/978-3-642-01777-3
|
| [17] |
K. Feng. Collected Works of Feng Kang (II), National Defence Press, Beijing, 1995.
|
| [18] |
K. Tselios, T. E. Simos. Runge-Kutta methods with minimal dispersion and dissipation for problems arising from computational acoustics, Journal of Computational and Applied Mathematics, 2005, 175(1), 173-181.
https://doi.org/10.1142/9789812704658_0142
|
| [19] |
L. Brusa, L. Nigro. A one-step method for direct integration of structural dynamic equations, International Journal for Numerical Methods in Engineering, 1980, 15(5), 685-699.
https://doi.org/10.1002/nme.1620150506
|
| [20] |
M. Z. Qin, M. Q. Zhang. Symplectic Runge-Kutta algorithmz for Hamilton systems, Journal of Computational Mathematics, Supplementary Issue, 1992, 205-215.
|
| [21] |
P. J. van der Houwen, B. P. Sommejier. Phase-lag analysis of implicit Runge-Kutta methods, SIAM J. Numer. Anal, 1989, 26(1), 214-229,
https://doi.org/10.1137/0726012
|
| [22] |
Run-de Zhang, Le-ping Yang, Wei-wei Cai. Symplectic Runge-Kutta Method Based Numerical Solution for the Hamiltonian Model of Spacecraft Relative Motion, Springer Nature Singapore Pte Ltd, 2019,
https://doi.org/10.1007/978-981-13-3305-7_171
|
| [23] |
U. Ascher, S. Reich. On some difficulties in integrating highly oscillatory Hamiltonian systems, in Computational Molecular Dynamics, Lecture Notes in Comput. Sci. Engrg. 4, Springer, Berlin, 1999, 281-296.
|
| [24] |
V. I. Amold. Mathematical Methods of Classical Mechanics, Springer-Berlin, 1999.
|
| [25] |
Y. B. Suris. Canonical transformation generated by methods of Runge-Kutta type for the numerical integration of the system x´´=-∂U/∂x, Zhurnal Vychisliteli Matermatiki I Mathematics, 2005, 175(1), 173-181.
|
| [26] |
Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods of fifth and sixth order, The Scientific World Journal, 2014,
https://doi.org/10.1155/2014/147801
|
| [27] |
Y. H. Cong, C. X. Jiang. Diagonally Implicit Symplectic Runge-Kutta Methods with High Algebraic and Dispersion Order, The Scientific World Journal, 2014, Article ID 147801, 7,
http://dx.doi.org/10.1155/2014/147801
|
| [28] |
Y. L. Fang, Q. H. Li. A class of explicit rational symplectic integrators, Journal of Applied Analysis and Computation, 2012, 2(2), 161-171.
https://doi.org/10.11948/2012012
|
| [29] |
Z. Kalogiratou, Th. Monovasilis. Diagonally Implicit Symplectic Runge-Kutta Methods with Special Properties, Appli. Mathe. & Infor. Scie, Feb. 2015,
http://dx.doi.org/10.12785/amis/091L02
|
| [30] |
Z. Kalogiratou, T. Monovasilis, T. E. Simos. A diagonally implicit symplectic Runge-Kutta method with minimum phase-lag, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 11), vol. 1389 of AIP Conference Proceedings, 2011, 1977-1979,
https://doi.org/10.1063/1.3637001
|
| [31] |
Z. Kalogiratou, T. Monovasilis, T. E. Simos. Diagonally implicit symplectic Runge-Kutta method with special properties, in Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM 12), 1479 of AIP Conference Proceedings, 2012, 1387-1390,
https://doi.org/10.1063/1.4756416
|
Cite This Article
-
-
@article{10.11648/j.engmath.20230701.12,
author = {Thae Gun Oh and Ji Hyang Choe and Jin Sim Kim},
title = {Diagonally Implicit Symplectic Runge-Kutta Methods with 7th Algebraic Order
},
journal = {Engineering Mathematics},
volume = {7},
number = {1},
pages = {19-28},
doi = {10.11648/j.engmath.20230701.12},
url = {https://doi.org/10.11648/j.engmath.20230701.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.engmath.20230701.12},
abstract = {The numerical integration of Hamiltonian systems with oscillating solutions is considered in this paper. Since Hamiltonian systems have good properties such as symplecticity, numerical methods that preserve these properties have attracted the great attention. In fact, the explicit Runge-Kutta methods have used due to that schemes are very simple and its computational amounts are very small. However, the explicit schemes aren’t stable so the implicit Runge-Kutta methods have widely studied. Among those implicit schemes, symplectic numerical methods were interested. It is because it has preserved the original property of the systems. So, study of the symplectic Runge-Kutta methods have performed. The typical symplectic Runge-Kutta method is the Gauss-Legendre method, whose drawback is that it is a general implicit scheme and is too computationally expensive. Despite these drawbacks, the study of the diagonally implicit symplectic Runge-Kutta methods that preserves symplecticity has attracted much attention. The symplectic Runge-Kutta method has been studied up to sixth order in the past and efforts to obtain higher order conditions and algorithms are being intensified. In many applications such as molecular dynamics as well as in space science, such as satellite relative motion studies, this method is very effective and its application is wider. In this paper, it is presented the 7th order condition and derive the corresponding optimized method. So the diagonally implicit symplectic eleven-stages Runge-Kutta method with algebraic order 7 and dispersion order 8 is presented. Numerical experiments with some Hamiltonian oscillatory problems are presented to show the proposed method is as competitive as the existing same type Runge-Kutta methods.
},
year = {2024}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Diagonally Implicit Symplectic Runge-Kutta Methods with 7th Algebraic Order
AU - Thae Gun Oh
AU - Ji Hyang Choe
AU - Jin Sim Kim
Y1 - 2024/07/03
PY - 2024
N1 - https://doi.org/10.11648/j.engmath.20230701.12
DO - 10.11648/j.engmath.20230701.12
T2 - Engineering Mathematics
JF - Engineering Mathematics
JO - Engineering Mathematics
SP - 19
EP - 28
PB - Science Publishing Group
SN - 2640-088X
UR - https://doi.org/10.11648/j.engmath.20230701.12
AB - The numerical integration of Hamiltonian systems with oscillating solutions is considered in this paper. Since Hamiltonian systems have good properties such as symplecticity, numerical methods that preserve these properties have attracted the great attention. In fact, the explicit Runge-Kutta methods have used due to that schemes are very simple and its computational amounts are very small. However, the explicit schemes aren’t stable so the implicit Runge-Kutta methods have widely studied. Among those implicit schemes, symplectic numerical methods were interested. It is because it has preserved the original property of the systems. So, study of the symplectic Runge-Kutta methods have performed. The typical symplectic Runge-Kutta method is the Gauss-Legendre method, whose drawback is that it is a general implicit scheme and is too computationally expensive. Despite these drawbacks, the study of the diagonally implicit symplectic Runge-Kutta methods that preserves symplecticity has attracted much attention. The symplectic Runge-Kutta method has been studied up to sixth order in the past and efforts to obtain higher order conditions and algorithms are being intensified. In many applications such as molecular dynamics as well as in space science, such as satellite relative motion studies, this method is very effective and its application is wider. In this paper, it is presented the 7th order condition and derive the corresponding optimized method. So the diagonally implicit symplectic eleven-stages Runge-Kutta method with algebraic order 7 and dispersion order 8 is presented. Numerical experiments with some Hamiltonian oscillatory problems are presented to show the proposed method is as competitive as the existing same type Runge-Kutta methods.
VL - 7
IS - 1
ER -
 Copy
|
Copy
|
 Download
Download
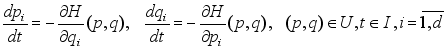 (1)
(1)